Question

What is the angle between the radius vector and the centripetal acceleration?
(A) $ \dfrac{\pi }{2} $
(B) $ 2\pi $
(C) $ \dfrac{{3\pi }}{2} $
(D) $ \pi $

Answer 1

Hint
Centripetal acceleration acts on a body moving in a circular path. It acts towards the centre of the body. The angle between this acceleration and the radius vector can be found by understanding their directions.

Complete step by step answer
Centripetal is similar to ‘central-seeking’. A force that is responsible for generating circular motion in a body is called centripetal force. As we know that force is calculated as the product of mass and acceleration that a body is going through, the acceleration produced by centripetal force is consequently, termed as centripetal acceleration. Since mass is directionless but force is a vector quantity, the direction of the centripetal acceleration is the same as the direction of the force i.e. towards the centre.
In a circular motion, the radius vector points towards the circumference of the motion. It starts from the centre and ends outwards on the surface of the circle.

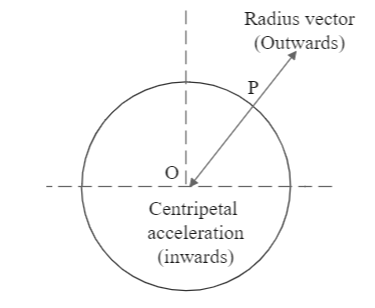
We can see that the centripetal acceleration acts towards the centre O, while the radius vector acts outwards from the centre towards point P. This implies that these two quantities have exactly opposite directions of operation. Hence, the angle between them is equal to $ \pi $ .
Option (D) is the correct answer.

Note
Centripetal acceleration can be observed with a simple experiment. Take a ball and tie a long thread around it. When you start swinging it using one end of the thread above your head or in front of your body, try to make circular motion. The system constantly moves in a circular path with the help of force provided by you. But the ball does not fall off because of the centripetal acceleration that acts inwards and keeps the system stable.