Question

An oxygen atom has a total of \[8\] electrons. How do you write the \[4\] quantum numbers for each of the \[8\] electrons in the ground state?

Answer 1

Hint: We have to know that the quantum is described as the set of numbers which is used to determine the position and energy of an electron present in the atom. There are a total of four quantum numbers. Principal quantum number, which is denoted as n, orbital angular quantum number (l), magnetic quantum number (\[{m_I}\]) and electron spin quantum number \[\left( {{m_s}} \right)\].

Complete answer:
The oxygen is a chemical compound having the atomic number,\[8\]and having the symbol, $'O'$. And the electronic configuration of oxygen is, \[1{s^2}2{s^2}2{p^4}\] and we can be represented as,

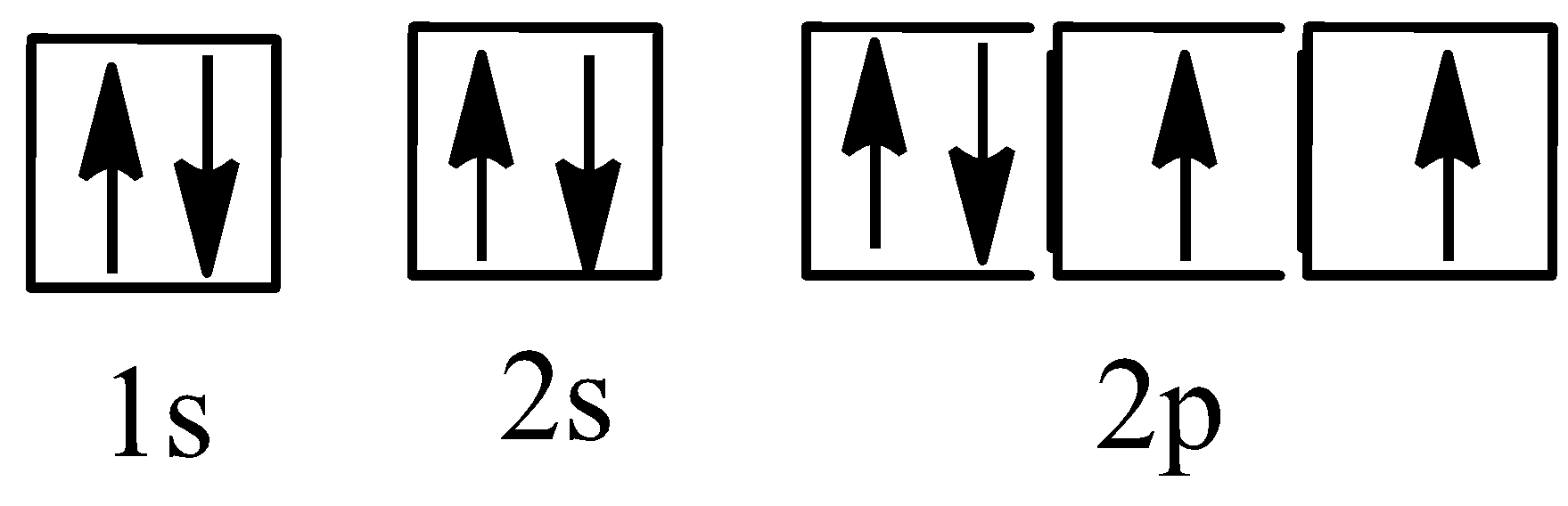
The \[4\]quantum numbers for each of the\[8\]electrons in the ground state can be written as,
The first energy level;
\[n = 1,l = 0,{m_l} = 0,{m_s} = - \dfrac{1}{2} \to \]The electrons located in the 1s orbital, spin – down
\[n = 1,l = 0,{m_l} = 0,{m_s} = + \dfrac{1}{2} \to \] The electrons located in the 1s orbital, spin – up
The second energy level;
\[n = 2,l = 0,{m_l} = 0,{m_s} = - \dfrac{1}{2} \to \] The electrons located in the 2s orbital, spin – down
\[n = 2,l = 0,{m_l} = 0,{m_s} = + \dfrac{1}{2} \to \] The electrons located in the 2s orbital, spin – up
\[n = 2,l = 1,{m_l} = - 1,{m_s} = - \dfrac{1}{2} \to \] The electrons located in the \[2{p_x}\] orbital, spin – down
\[n = 2,l = 1,{m_l} = - 1,{m_s} = + \dfrac{1}{2} \to \] The electrons located in the \[2{p_x}\] orbital, spin – up
\[n = 2,l = 1,{m_l} = 0,{m_s} = + \dfrac{1}{2} \to \] The electrons located in the \[2{p_y}\] orbital, spin – up
\[n = 2,l = 1,{m_l} = 1,{m_s} = + \dfrac{1}{2} \to \] The electrons located in the \[2{p_z}\] orbital, spin – up

Note:
We have to know that the principal quantum number determines the distance between the electrons and nucleus and it is directly proportional to the atomic size. The possible values of the principal quantum number may be \[1,2,3,4,...\] . Azimuthal quantum number also known as orbital angular momentum quantum numbers and the possible values of l is \[0,1,2,3,4,..,\left( {n - 1} \right)\]. The value of magnetic quantum \[{m_I}\]is equal to \[ - l,..., - 1,0,1...,l\]. And the possible values of electron spin quantum number\[\left( {{m_s}} \right)\]is \[ + \dfrac{1}{2}, - \dfrac{1}{2}\].