Question

An overhead water tanker in the shape of a cylinder has a capacity of 616 liters. The diameter of the tank is 5.6 m. Find the height of the tank.

Answer 1

Hint – We will solve this question by noting down all the information given in the question and by using this information we will draw a figure to make it look more easy. By using the formula of the Volume of the Cylinder, i.e., $\pi \times radiu{s^2} \times height$, will give us the result.

Complete step-by-step solution -
Here, in the question, given that, a water tanker in the shape of a Cylinder has Capacity or Volume of 616 liters and the diameter of this tank is 5.6 m.

So by using this, we can make a figure, which is as follows:

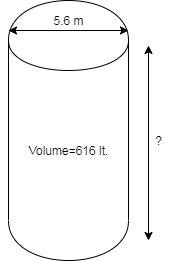
Now, let the height of the Cylinder be $h$.
Given that,
Capacity or Volume of the Cylinder = 616 lt.
 $
   = 616 \times 1000mililiters \\
   = 616000ml. \\
 $
 $ = 616000c{m^3}$ $\left[ {\because 1ml = 1c{m^3}} \right]$
Diameter of the Cylinder = 5.6 m
We know that,
$
  Diameter = 2 \times Radius \\
  \therefore Radius = \dfrac{{Diameter}}{2} \\
 $
Therefore, Radius of the Cylinder $ = \dfrac{{Diameter}}{2}$
                                                               $ = \dfrac{{5.6}}{2}$
                                                              $ = \dfrac{{56}}{{2 \times 10}}$
                                                              $ = 2.8m$
                                                              $ = 2.8 \times 100$cm
                                                              $ = 280cm$
Hence, Radius of the Cylinder = 280 cm.

Now, Capacity or Volume of the Cylinder = 616000$c{m^3}$
$
   \Rightarrow \pi \times Radiu{s^2} \times Height = 616000 \\
   \Rightarrow \dfrac{{22}}{7} \times {\left( {280} \right)^2} \times h = 616000 \\
   \Rightarrow \dfrac{{22}}{7} \times 280 \times 280 \times h = 616000 \\
   \Rightarrow \dfrac{{22}}{7} \times 78400 \times h = 616000 \\
   \Rightarrow 22 \times 11200 \times h = 616000 \\
   \Rightarrow 22 \times h = \dfrac{{616000}}{{11200}} \\
   \Rightarrow 22 \times h = 55 \\
   \Rightarrow h = \dfrac{{55}}{{22}} \\
   \Rightarrow h = \dfrac{5}{2} \\
   \Rightarrow h = 2.5cm \\
 $
Hence, the height of the cylinder is 2.5 cm.

Note – A cylinder is a closed solid that has two parallel bases joined by a curved surface, at a fixed distance. While solving these kinds of questions, one should not have any doubts related to the formula, otherwise there are chances of making mistakes.