Question

An optical bench has 1.5m long scale having four equal divisions in each cm. While measuring the focal length of a convex lens, the lens is kept at 75 cm mark of the scale and the object pin is kept at 45 cm mark. The image of the object pin on the other side of the lens overlaps with the image pin that is kept at 135 cm mark. In this experiment, the percentage error in the measurement of the focal length of the lens is.

Answer 1

Hint: In order 10 solve the problem, first we calculate the focal length of lens by using following formula
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
Where
u $ = $ distance of object from lens
v $ = $distance of image from lens
f $ = $ focal length of lens
After then differentiate the above equation and calculate the percentage error in the measurement of focal length.


Step by step answer: We can solve the problem with the help of diagrams easily.

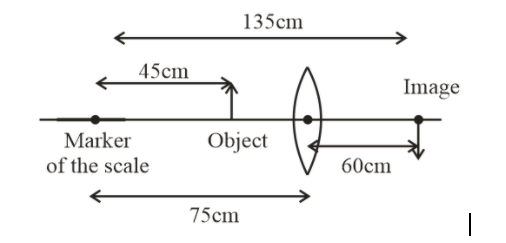
From figure, we can easily see the value of u and v i.e.,
u $ = $ distance of object from lens
$u = - (75 - 45)$
$u = - 30cm$
and
v $ = $ distance of image from lens
$v = 60cm$
We know that the lens formula
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ …..(!)
$\dfrac{1}{f} = \dfrac{1}{{60}} - \dfrac{1}{{( - 30)}}$
$\dfrac{1}{f} = \dfrac{1}{{60}} + \dfrac{1}{{30}}$
$\dfrac{1}{f} = \dfrac{{30 + 60}}{{(60)(30)}} = \dfrac{{90}}{{1800}}$
$\dfrac{1}{f} = \dfrac{1}{{20}}$
$f = 20cm$
Now, on differentiating equation 1
$ - \dfrac{{df}}{{{f^2}}} = - \dfrac{{dv}}{{{v^2}}} - \left( { - \dfrac{{du}}{{{u^2}}}} \right)$
$\dfrac{{df}}{{{f^2}}} = \dfrac{{dv}}{{{v^2}}} - \dfrac{{du}}{{{u^2}}}$
So, the maximum, error in f is
${\left( {\dfrac{{\Delta f}}{{{f^2}}}} \right)_{\max }} = \dfrac{{\Delta v}}{{{v^2}}} + \dfrac{{\Delta u}}{{{u^2}}}$
Here $\Delta v = $ error in measurement of v i.e., $\dfrac{1}{2}$ because there are 4 equal divisions in scale.
So, $\Delta f = {f^2}\left( {\dfrac{{\Delta v}}{{{v^2}}} + \dfrac{{\Delta u}}{{{u^2}}}} \right)$
$\Delta f = \dfrac{{400}}{2}\left[ {\dfrac{1}{{3600}} + \dfrac{1}{{900}}} \right]$
$\Delta f = 200\left[ {\dfrac{{1 + 4}}{{3600}}} \right] = 200 \times \dfrac{5}{{3600}}$
$\Delta f = \dfrac{{10}}{{36}}$
Hence, the $\% $ error in focal length is
$\dfrac{{\Delta f}}{f} \times 100\% = \dfrac{{10}}{{36 \times 20}} \times 100\% $
$ = \dfrac{{100}}{{72}}\% = 1.3888\% $
$\% $ error in $f \approx 1.39\% $


Note: There are some uses of optical bench experiment which are
1.To calculate the focal lengths of lenses.
2.Combine the lenses to demonstrate the principle of a telescope.