Question

An open U-tube contains mercury. When 11.2cm of water is poured into one of the arms of the tube, how high does the mercury rise in the other arm from its initial unit?
A. 0.56 cm
B. 1.35 cm
C. 0.41 cm
D. 2.32 cm

Answer 1

Hint: In order to solve the problem, use the concept of pressure and height. We know that the pressure on the outer surface of both the sides of the u tube will be atmospheric pressure and also we know that the pressure inside the same liquid at the same height will be equal. We will use this concept along with the formulas to solve the problem.
Formula used- \[P = {P_{\left( {ref} \right)}} + \rho gh\]

Complete Step-by-Step solution:
Given that 11.2cm of water is poured into one of the arms of the tube.
Figure:

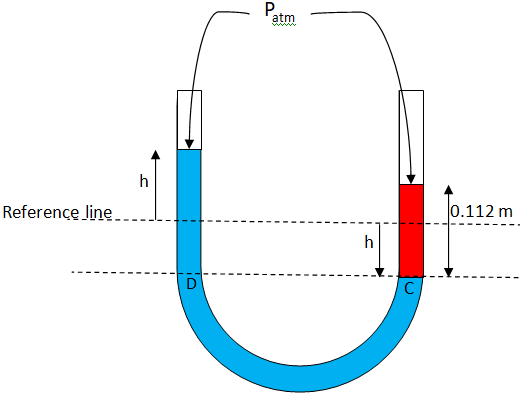
From figure:
Let assume that our reference line is the upper dotted line as mentioned in the figure.
Initially the water level was at the reference line.
When pouring the water in the right arm of the tube, the point C initially at the reference point then moves down to the lower dotted line. At the same time, the point D moves up from the reference line to the height h so the pressure at the point C will be equal to pressure at the point D
So, now the C point moves down h, and D point moves up h.
As we know that the pressure at any point with respect to any reference point is given as:
\[P = {P_{\left( {ref} \right)}} + \rho gh\]
From the figure:
Pressure at the point C with reference to the atmospheric pressure at the top is given as:
$
  \because P = {P_{\left( {ref} \right)}} + \rho gh \\
   \Rightarrow {P_C} = {P_{\left( {atm} \right)}} + {\rho _w}gh \\
   \Rightarrow {P_C} = {P_{\left( {atm} \right)}} + {\rho _w}g\left( {0.112} \right).......(1) \\
 $
Similarly pressure at the point D with reference to the atmospheric pressure at the top is given as:
$
  \because P = {P_{\left( {ref} \right)}} + \rho gh \\
   \Rightarrow {P_D} = {P_{\left( {atm} \right)}} + {\rho _m}gh \\
   \Rightarrow {P_D} = {P_{\left( {atm} \right)}} + {\rho _m}g\left( {h + h} \right) \\
   \Rightarrow {P_D} = {P_{\left( {atm} \right)}} + {\rho _m}g\left( {2h} \right)...........(2) \\
 $
As we know that the pressure inside the same liquid at the same height will be equal.
So in the mercury, the pressure at the point C is equal to pressure at the point D.
$ \Rightarrow {P_C} = {P_D}$
So, let us compare equation (1) and equation (2) in order to find the value of h.
$ \Rightarrow {P_{\left( {atm} \right)}} + {\rho _w}g\left( {0.112} \right) = {P_{\left( {atm} \right)}} + {\rho _m}g\left( {2h} \right).$
Let us solve the terms by cancelling the common terms.
\[
   \Rightarrow {\rho _w}g\left( {0.112} \right) = {\rho _m}g\left( {2h} \right) \\
   \Rightarrow 2h = \dfrac{{{\rho _w}g\left( {0.112} \right)}}{{{\rho _m}g}} \\
   \Rightarrow h = \dfrac{{{\rho _w}g\left( {0.112} \right)}}{{2{\rho _m}g}} \\
   \Rightarrow h = \dfrac{{{\rho _w}\left( {0.112} \right)}}{{2{\rho _m}}} \\
 \]
Let us substitute the values of density of mercury and water to solve for h.
The density of water is $1000kg/{m^3}$
And the density of mercury is $13600kg/{m^3}$
\[
   \Rightarrow h = \dfrac{{{\rho _w}\left( {0.112} \right)}}{{2{\rho _m}}} \\
   \Rightarrow h = \dfrac{{\left( {1000} \right)\left( {0.112} \right)}}{{2\left( {13600} \right)}} \\
   \Rightarrow h = 0.00412m = 0.412cm \\
 \]
Hence, the rise in the level of mercury in the other arm from its initial unit is 0.41 cm.
So, the correct answer is option C.

Note- Pressure is defined as a force per unit area-so the most effective way to calculate low air pressure is to place a column of known weight liquid against it and calculate so measured the height of the liquid column. The widely employed units of measurement are inches of mercury (in. Hg), using mercury as the liquid and inches of water, using gas or oil as the liquid. U tube manometer works on the same principle and is used to find the pressure.