Question

An open box is made of wood 3 cm thick. Its external length, breadth and height are 1.48m, 1.16m and 8.3dm. Find the cost of painting the inner surface if the cost of painting is Rs.50 per sq metre.

Answer 1

Hint: To solve this problem, we should know the formula related to the area of a rectangle. Area of a rectangle with the length and breadth as l and b units is given by the formula $\text{Area}=lb$sq units. In our question, we are asked the cost of painting the inner area, which means that we should find the area of the inner surface and multiply it by 50. From the below diagram, we can write that the length and breadth of the inner surface will be 3 + 3 = 6 cm thinner than the length and breadth of the outer surface. The height of the inner surface will be 3 cm less than the height of the outer surface as the box is an open one. Using the area of the rectangle, we can calculate the areas of the five faces and add them to get the total surface area of the inner surface and multiplying by 50 gives the answer. We should use all the values in the question after converting them to a single unit. We know that $\text{1m=100cm}$ and $\text{1dm=10cm}$. Using them, we can change all the values into centimetres and use them.

Complete step-by-step answer:

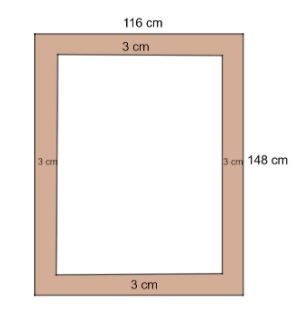
We are given an open box with its outer dimensions length, breadth and height as 1.48 m, 1.16 m and 8.3 dm respectively. We should use all the values in the question after converting them to a single unit. We know that $\text{1m=100cm}$ and $\text{1dm=10cm}$. Using them, we can change all the values into centimetres and use them. We can write the final length, breadth and height after changing the units into centimetres as 148 cm, 116 cm and 83 cm respectively. The thickness of the wood is 3 cm. We know that the length, width and height of the inner surface will be less than the outer dimensions. From the above diagram, we can infer that the length and breadth have decreased by two times the thickness.
So, we can write the dimensions of the inner surface as
Inner Length L = Outer length - $2\times $thickness $=148-2\times 3=142cm$
Inner breadth B = Outer breadth - $2\times $thickness $=116-2\times 3=110cm$
The dimensions of the inner height will be reduced by one thickness as the box is an open one and the difference is due to the bottom wood.
Inner Height H = Outer height - $1\times $thickness $=83-1\times 3=80cm$
The total area of the inner surface can be calculated using the area of the rectangle formula. Area of the rectangle with length and breadth as l and b respectively is given by the formula $\text{Area}=l\times b$.
We can infer that the inner surface of the box has 5 surfaces in total. The total surface area is the sum of all the areas of the 5 surfaces.
We know that the bottom surface has the inner length and the inner breadth as the length and breadth respectively. We know that two of the elevated surfaces have length and breadth as inner length and inner height whereas two of the elevated surfaces have inner breadth and inner height as the length and the breadth.
Total inner surface area$=L\times B+L\times H+L\times H+B\times H+B\times H$
$\begin{align}
  & =142\times 110+142\times 80+142\times 80+110\times 80+110\times 80 \\
 & =15620+11360+11360+8800+8800=15620+22720+17600=55940c{{m}^{2}} \\
\end{align}$
We know that $1m=100cm$
Converting the obtained area into sq m, we get
$Area=55940cm\times cm=55940\dfrac{1}{100}\times \dfrac{1}{100}{{m}^{2}}=5.594{{m}^{2}}$
We can infer from the question that the cost of 1 sq metre is Rs.50. We can write the cost of the required area as
$\text{Cost}=\text{Area}\times 50=5.594\times 50=\text{Rs}.279.7$
$\therefore $ The cost of painting the total inner surface is Rs. 279.7

Note: Students can make a mistake while dealing with different units. They generally forget to change the units and do the calculations which leads to a wrong answer. In this question, the height and thickness are in different units and we should put all the values into a single unit. At the end of the calculation, we should get them to the units which are asked in the question. It is always a good practice to write different parameters given in the question in the same unit and then start solving the question.