Question

An observer, 1.5 m tall, is 28.5 m away from a tower 30 m high. Determine the angle of elevation of the top of the tower from his eye.

Answer 1

Hint: To solve this question first we need to draw a diagram. We will use the trigonometric ratios and trigonometric functions to solve this question. We will use $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $ then substitute the values and solving

Complete step by step answer:
We have been given that an observer, 1.5 m tall, is 28.5 m away from a tower 30 m high.
We have to find the angle of elevation of the top of the tower from his eye.
Let us draw a diagram using the given information.

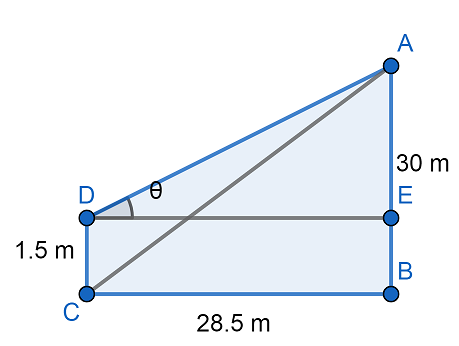
Here in this diagram let us assume that DC is the height of the observer which is given $ DC=1.5m $, the height of tower $ AB=30m $, the distance between observer and tower $ BC=28.5m $.
Now, let us assume the angle of elevation of the top of the tower from the eye of the observer will be $ \theta $.
Let us consider $ \Delta ADE $ ,
We know that $ \tan \theta =\dfrac{\text{perpendicular}}{\text{base}} $
Substituting the values we get
 $ \begin{align}
  & \Rightarrow \tan \theta =\dfrac{AE}{DE} \\
 & \Rightarrow \tan \theta =\dfrac{AB-BE}{DE} \\
\end{align} $
Now, from diagram we have DE=BC and DC=BE (parallel lines)
So, we get
 $ \Rightarrow \tan \theta =\dfrac{AB-BE}{BC} $
Now, we have $ AB=30m $ , $ BC=28.5m $ , $ BE=1.5m $
Substituting the values we get
 $ \Rightarrow \tan \theta =\dfrac{30-1.5}{28.5} $
Now, solving further we get
 $ \begin{align}
  & \Rightarrow \tan \theta =\dfrac{28.5}{28.5} \\
 & \Rightarrow \tan \theta =1 \\
\end{align} $
Now, we know that $ \tan 45{}^\circ =1 $
So, we get
  $ \begin{align}
  & \Rightarrow \tan \theta =\tan 45{}^\circ \\
 & \Rightarrow \theta =45{}^\circ \\
\end{align} $
So, the angle of elevation of the top of the tower from the eye of observer is $ 45{}^\circ $ .

Note:
Students can assume the angle of elevation at point C which is incorrect. As we have asked in the question that we have to find the angle of elevation from the eye of the observer and the observer is not a point object. So keep this in mind and solve the question carefully.