Question

An object of height $4.0cm$ is placed at a distance of $30cm$ from the optical centre 'O' of a convex lens of focal length $20cm$. Draw a ray diagram to find the position and size of the image formed. Mark optical centre 'O' and principal focus 'F' on the diagram. Also find the approximate ratio of size of the image to the size of the object.

Answer 1

Hint: Use the lens formula to find out the value of image distance. Thereafter, draw the whole apparatus as a ray diagram. Finally find the magnification and size of the image, which is related to the ratio of image distance and object distance.

Formula Used:
Lens equation is $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
And the magnification, $m = \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$

Complete step by step answer:
Given that an object of height $4.0cm$ is placed at a distance of $30cm$ from the optical centre 'O' of a convex lens of focal length $20cm$.
$u = - 30cm$ By sign convention since image is kept at the left of the lens
$f = + 20cm$
${h_i} = 4cm$
Using lens equation we get,
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$
$ \Rightarrow \dfrac{1}{v} = \dfrac{1}{f} + \dfrac{1}{u}$
We put the values of the known quantities
$ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{20}} + \dfrac{1}{{ - 30}}$
$ \Rightarrow \dfrac{1}{v} = \dfrac{1}{{60}}$
$ \Rightarrow v = + 60cm$
Thus the image is formed at the right side of the lens at a distance of $60cm$ from the lens.
Now we represent the above problem in a ray diagram

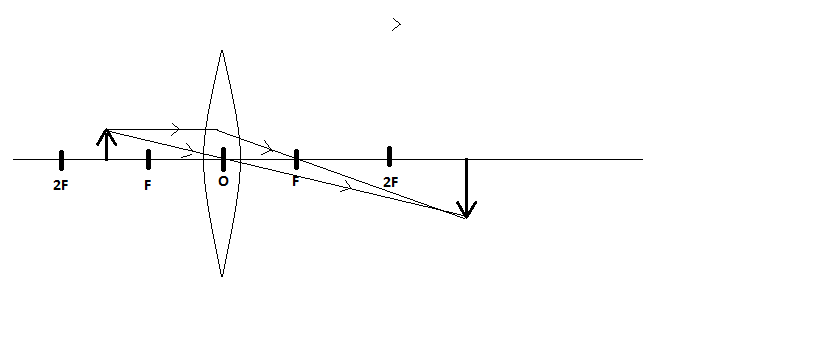
Here the optical centre 'O' and principal focus 'F' are marked on the diagram
Now we know that,
$m = \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$
$ \Rightarrow \dfrac{v}{u} = \dfrac{{{h_i}}}{{{h_o}}}$
Putting the values we get,
$ \Rightarrow \dfrac{{{h_i}}}{{{h_o}}} = \dfrac{{60}}{{ - 30}}$
$ \Rightarrow \dfrac{{{h_i}}}{{{h_o}}} = - 2$
The negative sign here shows that the image is inverted and hence real.
Thus the approximate ratio of size of the image to the size of the object is $2:1$
Again
$ \Rightarrow {h_i} = 2 \times {h_o}$ $ \Rightarrow {h_i} = 2 \times 4$
$ \Rightarrow {h_i} = 8cm$
Hence the size of image is $8cm$

Additional Information:
The mirror equation is given by
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Magnification in case of mirrors is given by
$m = \dfrac{{ - v}}{u} = \dfrac{{{h_i}}}{{{h_o}}}$

Note: Do all calculations properly. Do not use the mirror formula instead of the lens formula. Also keep in mind the sign convention. The top and right in the Cartesian plane corresponds to the positive direction and vice versa.