Question

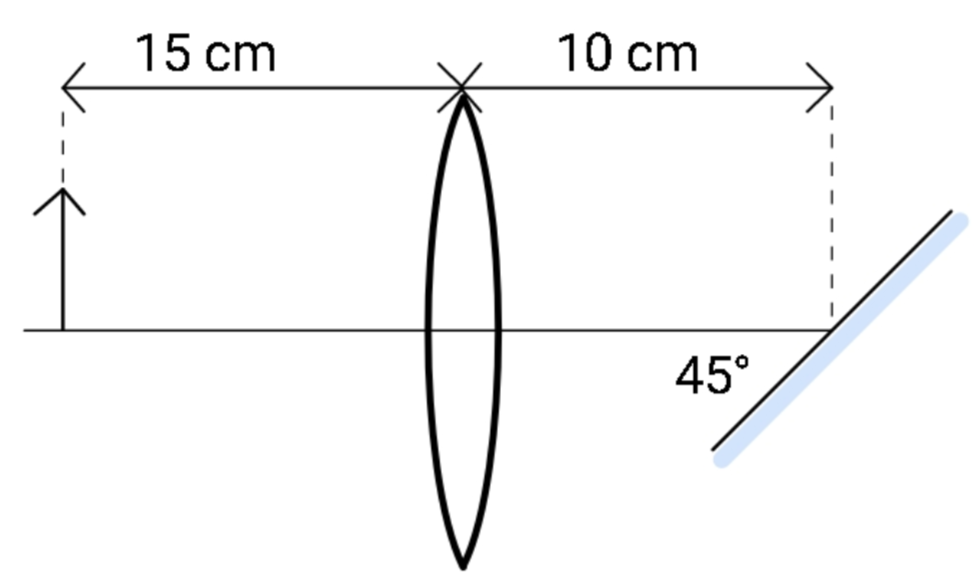
An object of height 4 cm is kept to the left of and on the axis of the converging lens of focal length 10 cm as shown in the figure. A plane mirror is placed at $45^{\circ}$ to the lens axis 10 cm to the right of the lens (see figure). Find the position and size of the image formed by combination.

Answer 1

Hint: Find the distance and height of the image by removing the plane mirror first. Apply laws of reflection from the plane mirror after that. A plane mirror forms a virtual image at a distance equal to the distance of the object in front of it.

Formula used:
Lens equation:
$\dfrac{1}{f} = \dfrac{1}{v} -\dfrac{1}{u} $
For the size of the image:
$\dfrac{H_I}{H_O} = - \dfrac{v}{u}$

Complete step-by-step solution:
First, let us consider the situation when the mirror was not in place.
We are given that the object is placed at a distance of 15cm from the lens and the focal length of the lens is 10 cm. Therefore we can write:
u = -15 cm and f = 10 cm for a convex lens.
$\dfrac{1}{v} = \dfrac{1}{f} +\dfrac{1}{u} $
Substituting the values:
$\dfrac{1}{v} = \dfrac{1}{10cm} +\dfrac{1}{-15cm} $
Or
$v = \dfrac{-15 \times 10}{-15 + 10}$cm = +30 cm.
Now, to find the size of the image, the formula for magnification for convex lens is used:
$M = \dfrac{H_I}{H_O} = - \dfrac{v}{u}$
where $H_I$ is height of the image,
$H_O$ is height of the object, v is the image distance and u is object distance.
We can modify this formula as:
$H_I = - \dfrac{v}{u} \times H_O$
Where we know the values u = 15 cm, v = 30 cm, and $H_O = 4$cm.
Keeping these values,
$H_I = - \dfrac{30}{15} \times 4$cm
$H_I = -8$cm
Therefore the size of the image is 8 cm. The image formed will be inverted.

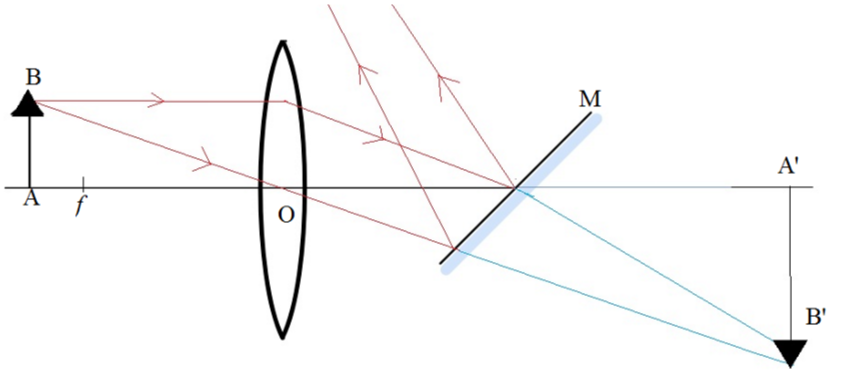
Now, if we place a mirror at another focus of the lens then the light will be reflected off the mirror and will create a real image when obtained on the screen. The plane mirror is not giving any additional path difference to the rays falling on it. It is just sending the light in a different direction. If we reproduce its path behind the mirror, we will be able to see that the image behind the mirror is just like the one formed by the lens.

Note: The sign conventions dictate that the distances measured in the ray direction are taken as positive and distances measured opposite to the ray direction are taken negatively. The focal length of a convex lens is always positive and the object distance is taken as negative. The height of the object above the principal axis is taken as positive and the height of the image below the principal axis will be negative.