Question

An object is placed at a distance of $30\;{\rm{cm}}$ from a concave mirror of focal length $20\;{\rm{cm}}$. Where will the image be formed? Draw the corresponding ray diagram.

Answer 1

Hint: Here, we will be using the formulas of the focal length for the mirror in which a relationship is established between the focal length of a mirror, distance of object from the mirror and distance of the image from the mirror.

Complete step by step answer:
Given, the focal length of the concave mirror is$f = - 20\;{\rm{cm}}$.
The distance of object from the mirror is $u = - 30\;{\rm{cm}}$
Substitute the value $f = - 20\;{\rm{cm}}$ and $u = - 30\;{\rm{cm}}$ in the mirror formula $\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$ to obtain the value of$v$.
$
\dfrac{1}{{ - 20}} = \dfrac{1}{{ - 30}} + \dfrac{1}{v}\\
\Rightarrow\dfrac{1}{v} = \dfrac{1}{{30}} - \dfrac{1}{{20}}\\
\Rightarrow\dfrac{1}{v} = \dfrac{{20 - 30}}{{600}}\\
\therefore v = - 60\;{\rm{cm}}
$
The position of the image is $60\;{\rm{cm}}$ left side (towards the object side) from the pole of the concave mirror which is represented in the following diagram. The image is straight and larger than the object. The corresponding ray diagram given below which shows the position of the image formed.

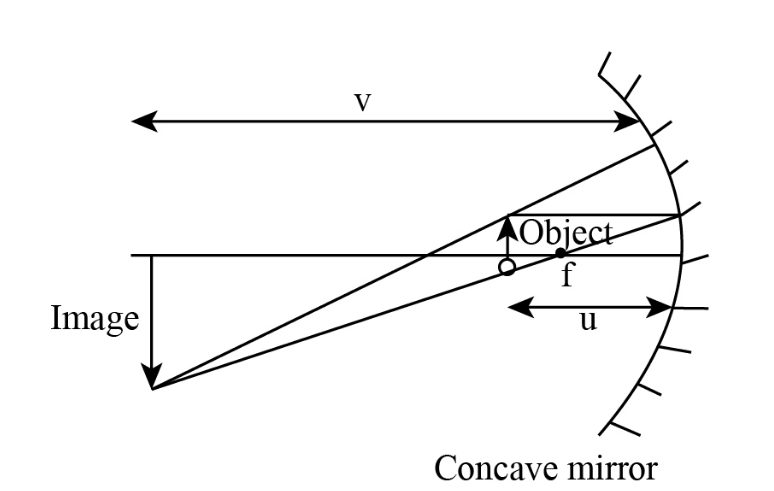
From the above ray diagram one can observe that the size of the image is larger than the size of the object and the position of the object is at $60\;{\rm{cm}}$ left side from the concave mirror. The formed image is opposite in shape compared to object orientation and the size of image is also larger than the size of the object.

Note: In these types of problems one thing should be remember that for the concave mirror the value of the distance of object from the mirror $u$ and distance of object from the mirror $f$ should be takes as negative value whereas for the convex mirror these two values should be taken as positive while using the focal length formula. Also there is no need to convert the units to SI units.