Question

An object has moved through a distance. Can it have a zero displacement? If yes, support the answer with an example.

Answer 1

Hint: Distance is a scalar quantity which has only magnitude whereas displacement is a vector quantity which has both magnitude and direction.

Complete step by step answer:
Distance: It is a total path length travelled by an object from its starting point to ending point.
Displacement: It is a change in position and we also define it as the shortest distance between the initial and final position of an object.
If ${{x}_{1}}$is the initial position of the object and ${{x}_{2}}$ is the final position of the object, then we can say that displacement is given by the difference of these two positions ,i.e.,
displacement, $\Delta x={{x}_{2}}-{{x}_{1}}$
Now by keeping the definitions in mind, let us try to solve the above question,
The answer is yes, an object can have zero displacement even though it is moved through a certain distance, since displacement is a change in position and it depends only on the final and initial position and not on the path taken.
So, if an object starts from point A and after travelling some distance it comes back to the same point A, then there is no change in position, so displacement is zero.
We can also conclude this by using above formula,
If initial position and final positions are same then,
$\begin{align}
  & {{x}_{1}}={{x}_{2}} \\
 & \Delta x={{x}_{1}}-{{x}_{1}}=0 \\
\end{align}$
Thus, displacement is zero, if initial and final positions are the same even though it travelled some distance.
We can give our day to day examples for this,
Consider a man walking from a point A, 4m towards right and 2m down and again to his initial position which is at a distance 6m as shown below -

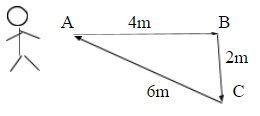
In this case, he travels a total distance of 12 m, but he came back to the same point where he started so his displacement is zero.
Like this, we can give an example of a car which is moving in a circular path, if it makes one circle and stops where it started, then it covers a distance of $2\pi r$(where r is a radius of that circle) but has zero displacement.

Additional information:
The magnitude of the displacement may or may not be equal to pathlength traversed by an object as it is the shortest distance between two points.
Whenever there is motion there is always distance so it is always positive but there may be or may not be displacement whenever there is motion, so displacement can be positive, negative and can be zero depending on the reference point.
SI units of distance and displacement is metre (m)

Note: Students may make mistakes by thinking that displacement cannot be zero as there is motion but if the starting point and ending point of an object are the same then displacement is always zero.
$\Delta x={{x}_{2}}-{{x}_{1}}$, in this if ${{x}_{1}}$ is greater than ${{x}_{2}}$, then displacement is negative and when ${{x}_{1}}$is less than ${{x}_{2}}$ it is positive, finally when both are equal it is above case i.e., displacement becomes zero.