Question

An inverted bell lying at the bottom of a lake $47.6\;m$ deep has $50\;cm^3$ of air trapped in it. The bell is brought to the surface of the lake. The volume of the trapped air will be (atmospheric pressure $=70\;cm$ of Hg and density of Hg$=13.6\;g/cm^3$
A. $300\; cm^3$
B. $800\;cm^3$
C. $900\;cm^3$
D. $200\;cm^3$

Answer 1

Hint: Here, since the bell is moved from the base of the lake to the surface, clearly the pressure on the bell varies and hence the volume. Then from Boyle’s law, we know that is PV is constant, we can use this to solve the problem and hence find the volume inside the bell when it is moved from the base to the surface.

Formula used: $PV=constant$

Complete step by step answer:
Consider the figure shown below, let the volume in the bell at the base be $V_1$ and on the surface be $V_2$.

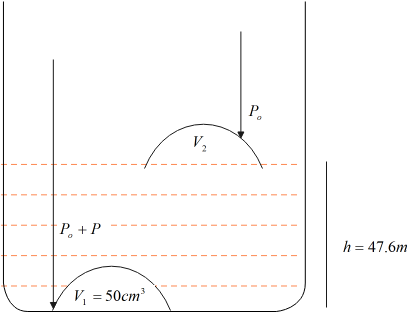
Clearly, the pressure exerted on the bell on the surface of the lake is just the atmospheric pressure $P_0$ . Since fluids exert pressure, which depends on the height of the fluid above the object, then the pressure exerted on the bell at the base is given as $P_0+P$where, $P$ is the fluid pressure.
We know that fluid pressure $P$ depends on the fluid and is mathematically expressed as $P=\rho_f\times g\times h_f$ Here, $\rho_f$ is the density of the fluid, $h_f$ is the height of the fluid and $g$ is the acceleration due to gravity.
From Boyles law we know that at constant temperature and number of moles, PV is a constant .
Then we have $P_0V_2=(P_0+P)V_1$
Given that $P_0=70cm$, $\rho_f=13.6g/cm^3$ and $h_f=47.6cm$ , then,
$P=1\times 4760$ , as the density of water in a lake is $1\;g/cm^3$, substituting, we have
$13.6 \times 70\times V_2=(70\times 13.6+ 4760)50$
$\implies V_2=\dfrac{(70\times 13.6+ 4760)50}{13.6\times70}$
$\implies V_2=300cm^3$
So, the correct answer is “Option A”.

Note: Here, the atmospheric pressure is in terms of Hg and hence when taking $P_0$ we take, $P_0=\rho_{Hg}\times g\times H$. Be careful while calculating the answer, as there can be some calculation error. Also always convert all the units to any one single unit, here everything is taken in cm.