Question

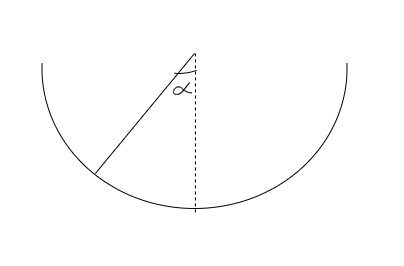
An insect crawls up a hemispherical surface very slowly as shown in figure. The coefficient of friction between the insect and the surface is $\dfrac{1}{3}$. If the line joining the centre of the hemispherical surface to the insect makes an angle $\alpha $with the vertical, the maximum possible value of $\alpha $ is given by-

$
  A.{\text{ cot}}\alpha {\text{ = 3}} \\
  {\text{B. sec}}\alpha {\text{ = 3}} \\
  {\text{C. cosec}}\alpha {\text{ = 3}} \\
  {\text{D. none}} \\
 $

Answer 1

- Hint- Here we will proceed by using the formula of force i.e. mg. and the formula of limiting friction i.e. ${f_l} = \mu N$ as here f is the maximum and limiting friction. Then we will equate both the equations formed to get the required result.

Complete step-by-step solution -
FORMULA USED-
$F = mg$
${f_l} = \mu N$
$\dfrac{1}{{\tan \theta }} = \cot \theta $

Here, given that-
The coefficient of friction between the insect and the surface i.e.$\mu = \dfrac{1}{3}$.
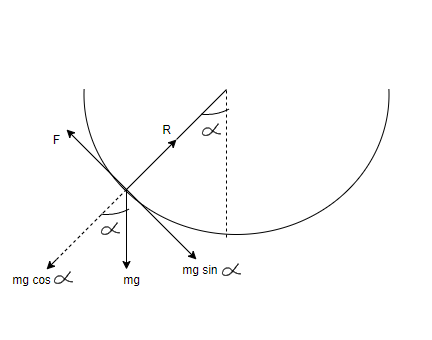
Now as we know that below the point at which insect will definitely have some mass, so force at that point will be mg.
$ \Rightarrow F = mg$
Also given that the the line joining the centre of the hemispherical surface to the insect makes an angle $\alpha $with the vertical, so mg will have two components-
$mg{\text{ sin}}\alpha $ ( which is downwards to mg)
$mg{\text{ cos}}\alpha $( which is upwards to mg, equal and opposite to normal)
As we know that in the diagram, $mg{\text{ sin}}\alpha $will balance static frictional force $f$(which is also maximum and limiting frictional force in this case of insect because after this point insect will start slipping)
Here, we must understand that only two forces are acting on insect,
Normal force
Mg force
So we get- $N = mg{\text{ cos}}\alpha ................\left( 1 \right)$
Now we will calculate limiting frictional force,
$f = mg{\text{ sin}}\alpha ...............\left( 2 \right)$
But we know that the formula of limiting friction i.e.${f_l} = \mu N$.
Where $\mu $ is coefficient of friction.
N is a normal reaction force.
Now using equation 1,
We get-
${f_l} = \mu mg{\text{ cos }}\alpha ........\left( 3 \right)$
In this question,
$f$ is the limiting frictional force$\left( {{f_l}} \right)$
So equating equation 2 and equation 3,
We get-
$mg{\text{ sin}}\alpha {\text{ = }}\mu {\text{ mg cos}}\alpha $
$\Rightarrow \sin \alpha = \mu \cos \alpha $
$\Rightarrow \dfrac{{\sin \alpha }}{{\cos \alpha }} = \mu $
$\Rightarrow \tan \alpha {\text{ = }}\mu $
$\Rightarrow \tan \alpha = \dfrac{1}{3}$ $\left( {\because \mu = \dfrac{1}{3}} \right)$
By cross-multiplying,
We get-
$\dfrac{1}{{\tan \alpha }} = 3$
$\cot \alpha = 3$ $\left( {\dfrac{1}{{\tan \theta }} = \cot \theta } \right)$
Therefore, option A is correct.

Note- While solving this question, we must know that here $f$ (static frictional force) will be the same as limiting frictional force ${f_l}$. Also, here we must understand that there are two forces i.e. normal force, mg force acting on insects. Hence we get our desired result.