Question

An insect $8m$ away from the foot of a lamp post which is $6m$ tall, crawls towards it. After moving through a distance, its distance from the top of the lamp post is equal to the distance it has moved. How far is the insect away from the foot of the lamp post?

Answer 1

Hint: Draw a diagram using all the information given in the question. Assume the pole to be perpendicular to the ground. This will give you two right-angled triangles. Consider the distance travelled by the insect as some variable$n$. Now use the Pythagoras theorem to figure out the value of $n$.

Complete step-by-step answer:

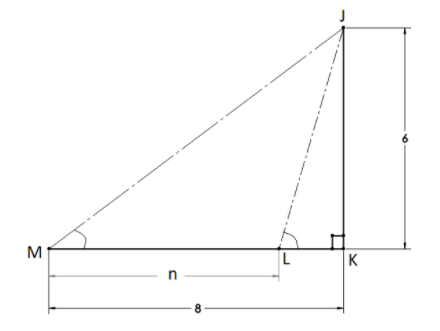
Let’s draw a diagram with all the given information first.
Suppose the insect starts from point M and moves toward the pole, i.e. JK which is of length $6m$ .
The distance from the base point to the initial position of the insect, i.e. MK is of length $8m$.
From point M insect moves towards the pole till point L. According to the question, length travelled is equal to the distance from the top of the pole, i.e. $ML = LJ$
We can assume that $ML = LJ = n,{\text{ therefore }} MK = n + LK \Rightarrow LK = \left( {8 - n} \right){\text{ m}}$
Also, since the pole is erected perpendicularly with the ground, we can say that the triangles $\Delta JKM {\text{ and }}\Delta JKL$ are right-angled triangles.
And the angle $\angle K$ is a right angle, i.e. $\angle JKM = \angle JKL = 90^\circ $
Now, we can consider the triangle $\Delta JKL$ and use Pythagoras’ theorem in that.
The Pythagoras theorem, also known as the Pythagorean theorem, states that the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle. Or, the sum of the squares of the two legs of a right triangle is equal to the square of its hypotenuse.
Here, we have hypotenuse as side JL and other sides as LK and JK.
$ \Rightarrow J{L^2} = J{K^2} + L{K^2}$
Now, we can substitute the values in this equation
$ \Rightarrow {n^2} = {6^2} + {\left( {8 - n} \right)^2}$
This can be further simplified using ${\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}$, and we get
$ \Rightarrow {n^2} = {6^2} + {8^2} - \left( {2 \times 8 \times n} \right) + {n^2}$
We can easily simplify to find the value of $n$
$ \Rightarrow {n^2} = 36 + 64 - 16n + {n^2} \Rightarrow 16n = 100 \Rightarrow n = \dfrac{{100}}{{16}} = 6.25 {\text{ m}}$
Therefore, the length $LK = 8 - n = 8 - 6.25 = 1.75 {\text{ m}}$
Hence, we get the distance from the base of the pole as $1.75 {\text{ m}}$

Note: Try to understand the problem using a diagram. Be careful while solving for the value of $n$. An alternative approach to the same problem could be taken by considering length LK as some variable $n$ and then$ML = LJ = \left( {8 - n} \right)$ . Using this assumption, you can directly get the answer after evaluating the value of $n$.