Question

An inclined plane is inclined at an angle $\theta$ with the horizontal. A body of mass $m$ rests on it, if the coefficient of friction is $\mu $, then the minimum force that has to be applied to the inclined plane to make the body just most up the inclined plane is-
A. $\mu mg\cos \theta $
B. $mg\sin\theta $
C. $\mu mg\cos \theta- mg\sin \theta $
D. $\mu mg\cos \theta + mg\sin \theta $

Answer 1

Hint: Draw the free body diagram of the given question by assuming the inclined plane as a triangle with the angle of $\theta$. Mark the $x$ and $y$ components of the body.

Step by Step Solution:
When a body is inclined with a plane at an angle of $\theta $ its force can be distributed into two different components. Now, the free body diagram can be drawn as given below,

     

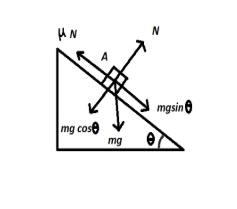
In the above given figure,
$\mu $ is the coefficient of friction, $N$ is the force acting, $m$ is the mass of the inclined body, $g$ is the acceleration due to gravity and$\theta $ is the angle of inclination.
Now, the force acting due to the body of mass $m$ is $mg$. Dissipating it into the $x$ and $y$ components, we get $mg\sin \theta $ and $mg\cos \theta $ respectively. The force acting in the opposite direction in order to pull the mass just up to the inclined plane would be $\mu N$.
Now, from the figure A, we can see that
$N = mg\cos \theta $, since they both are in the opposite direction
Therefore, in order to make the body just most up the inclined plane, a force greater than $mg\sin \theta $ should be applied,
Therefore,
${F_ {\min}} = \mu N - mg\sin \theta $
Where ${F_ {\min}}$ is the minimum force required to move the body just up the inclined plane.
We know that
$N = mg\cos \theta $
Therefore,
${F_ {\min}} = \mu mg\cos \theta - mg\sin \theta $
So, the net force along the inclined plane is $\mu mg\cos \theta - mg\sin \theta $
Therefore,
The minimum force required to move the body just up the inclined plane is $\mu mg\cos \theta - mg\sin \theta $
Or option C.

Note: The minimum force required to push the body up the incline plane. It must be equal to the net maximum force acting along the plane of incline. The friction for which the body does not move is called the static friction. The friction for which the body moves is called the kinetic friction. The minimum force required will be equal to maximum value of friction.