Question

An ideal monatomic gas gets expanded into twice its volume. If the process is isothermal, the magnitude of work done by the gas is ${{W}_{i}}$​. If the process is adiabatic, the magnitude of work done by the gas is ${{W}_{a}}$​. Which of the following will be true?
$\begin{align}
  & A.{{W}_{i}}={{W}_{a}}\rangle 0 \\
 & B.{{W}_{i}}\rangle {{W}_{a}}=0 \\
 & C.{{W}_{i}}\rangle {{W}_{a}}\rangle 0 \\
 & D.{{W}_{i}}={{W}_{a}}=0 \\
\end{align}$

Answer 1

Hint: Here the volume is getting expanded to twice of its value. The isothermal process is the process where the temperature is kept constant. An adiabatic process is explained as a process happening without any transfer of mass or heat energy between a thermodynamic system and its surroundings. It is different from an isothermal process, since it transfers energy to the surroundings only in the form of work.

Complete answer:

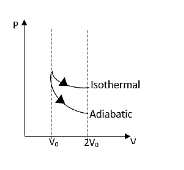
From this P-V diagram, we can conclude that, the isothermal lines are always higher than the adiabatic lines and they both starts and ends at the equal volume
And also the area under the isothermal line is higher than the adiabatic line. As we all know that the area under P-V diagram is referred to as the work done. Therefore we can write that,
\[{{W}_{i}}\langle {{W}_{a}}\]
It is obvious here that the gas is doing some kind of work that is why there is an area under the graph. Therefore we can conclude that,
\[{{W}_{i}}\rangle {{W}_{a}}\rangle 0\]

So, the correct answer is “Option C”.

Note:
In order to reach an equal height in a larger distance is given by the lower slope of the line. Therefore the adiabatic curve is steeper than the Isothermal curve. And also the adiabatic curve is having a specific value of slope which is higher than zero.