Question

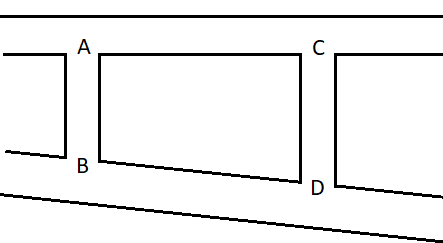
An ideal liquid is flowing in 2 pipes AC and BD. One is inclined and the second is horizontal. Both the pipes are connected by 2 vertical tubes. Assuming streamlines flow everywhere, if velocity of liquid at A, B and C are $ 2m/s $, $ 4m/s $ and $ 4m/s $ respectively, what will be the velocity at D.

Answer 1

Hint
Here we can use Bernoulli's theorem to find the equation of the flow of water at the points A, B, C and D. Then we can write the equations as point A and C as equal and from there find the pressure difference between point A and C. Using that in the equations of point B and D we can find the answer.
In this solution we will be using the following equation,
 $\Rightarrow P + \dfrac{1}{2}\rho {v^2} + h\rho g = {\text{constant}} $
where $ P $ is the pressure,
 $ \rho $ is the density of the liquid
 $ v $ is the velocity of the liquid
 $ h $ is the height and $ g $ is the acceleration due to gravity.

Complete step by step answer
Let us consider the height between the points A and B is $ {h_1} $ and that between the points C and D is $ {h_2} $. According to Bernoulli's theorem, for steady, irrotational motion of a fluid, the addition of the pressure head, kinetic energy head and the gravitational head is constant.
Therefore we can write, $ P + \dfrac{1}{2}\rho {v^2} + h\rho g = {\text{constant}} $
We consider the pressure at the point A, B, C and D $ {P_A} $, $ {P_B} $, $ {P_C} $ and $ {P_D} $ respectively and the velocities as, $ {v_A} $, $ {v_B} $, $ {v_C} $ and $ {v_D} $ .
Therefore, according to the figure, we can write the equation for the points A and C as,
 $\Rightarrow {P_A} + \dfrac{1}{2}\rho {v_A}^2 + {h_1}\rho g = {\text{constant}} $ for the point A.
and $ {P_C} + \dfrac{1}{2}\rho {v_C}^2 + {h_2}\rho g = {\text{constant}} $ for the point C.
We can equate them and hence get,
 $\Rightarrow {P_A} + \dfrac{1}{2}\rho {v_A}^2 + {h_1}\rho g = {P_C} + \dfrac{1}{2}\rho {v_C}^2 + {h_2}\rho g $
We take the terms containing $ {h_1} $ and $ {h_2} $ to the RHS and get,
 $\Rightarrow {P_A} + \dfrac{1}{2}\rho {v_A}^2 = {P_C} + \dfrac{1}{2}\rho {v_C}^2 + \left( {{h_2} - {h_1}} \right)\rho g $
We can take the pressure terms and bring them to the LHS and take the rest terms to RHS and get
 $\Rightarrow {P_A} - {P_C} = \dfrac{1}{2}\rho \left( {{v_C}^2 - {v_A}^2} \right) + \left( {{h_2} - {h_1}} \right)\rho g $
Similarly the Bernoulli’s equation for the points B and D are
 $\Rightarrow {P_B} + \dfrac{1}{2}\rho {v_B}^2 = {\text{constant}} $, as there is no height.
and $ {P_D} + \dfrac{1}{2}\rho {v_D}^2 = {\text{constant}} $
Equating these two we get,
 $\Rightarrow {P_B} + \dfrac{1}{2}\rho {v_B}^2 = {P_D} + \dfrac{1}{2}\rho {v_D}^2 $
Now we can write the pressure at point B is equal to, $ {P_B} = {P_A} + {h_1}\rho g $
and the pressure at the point D is equal to $ {P_D} = {P_C} + {h_2}\rho g $
So substituting these in the equation we get,
 $\Rightarrow {P_A} + {h_1}\rho g + \dfrac{1}{2}\rho {v_B}^2 = {P_C} + {h_2}\rho g + \dfrac{1}{2}\rho {v_D}^2 $
Now we bring the pressure terms to the LHS and take the other terms to the RHS and get,
 $\Rightarrow {P_A} - {P_C} = \left( {{h_2} - {h_1}} \right)\rho g + \dfrac{1}{2}\rho \left( {{v_D}^2 - {v_B}^2} \right) $
Now in place of $ {P_A} - {P_C} $ we can substitute $ {P_A} - {P_C} = \dfrac{1}{2}\rho \left( {{v_C}^2 - {v_A}^2} \right) + \left( {{h_2} - {h_1}} \right)\rho g $
Therefore, we get
 $\Rightarrow \dfrac{1}{2}\rho \left( {{v_C}^2 - {v_A}^2} \right) + \left( {{h_2} - {h_1}} \right)\rho g = \left( {{h_2} - {h_1}} \right)\rho g + \dfrac{1}{2}\rho \left( {{v_D}^2 - {v_B}^2} \right) $
The term $ \left( {{h_2} - {h_1}} \right)\rho g $ gets cancelled from both sides of the equation. Therefore we have,
 $\Rightarrow \dfrac{1}{2}\rho \left( {{v_C}^2 - {v_A}^2} \right) = \dfrac{1}{2}\rho \left( {{v_D}^2 - {v_B}^2} \right) $
Further cancelling the $ \dfrac{1}{2}\rho $ from both sides we get,
 $\Rightarrow {v_C}^2 - {v_A}^2 = {v_D}^2 - {v_B}^2 $
Now keeping the velocity of water at the point D on one side and taking all the other terms to the other side we get,
 $\Rightarrow {v_D}^2 = {v_C}^2 - {v_A}^2 + {v_B}^2 $
In the question we are given $ {v_A} = 2m/s $, $ {v_B} = 4m/s $ and $ {v_C} = 4m/s $
Therefore, substituting the values we get,
 $\Rightarrow {v_D}^2 = {\left( 4 \right)^2} - {\left( 2 \right)^2} + {\left( 4 \right)^2} $
On doing the squares and adding, the value we get is,
 $\Rightarrow {v_D}^2 = 16 - 4 + 16 = 28 $
Therefore, taking square root on both sides,
 $\Rightarrow {v_D} = \sqrt {28} m/s $
Hence the velocity of water at the point D is $ \sqrt {28} m/s $ .

Note
Bernoulli's theorem in fluid dynamics is a relation between the pressure, velocity and the elevation of the moving fluid where we consider the fluid to be incompressible, having negligible viscosity and in a steady irrotational flow. It can be derived from the law of conservation of energy, which states that in a steady flow, the sum of all forms of energy in a fluid along a streamline is the same at all points.