Question

An ideal elastic rubber ball is dropped from a height, about 2 meters, hits the floor and rebounds to its original height. Which of the following graphs would best represent the distance above the floor versus time for the above bouncing ball?

A.

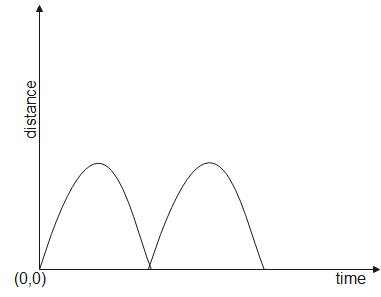
B.

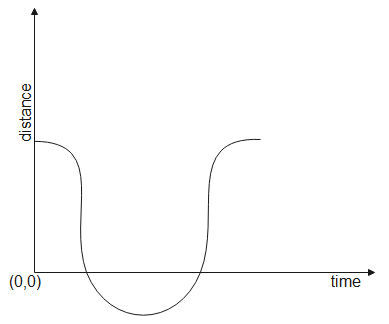
C.

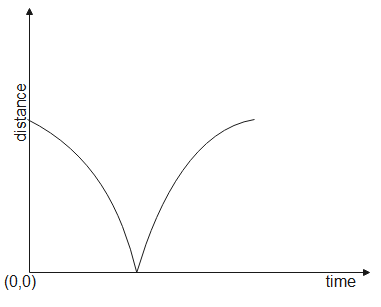
D. None of these

Answer 1

Hint: In case of collisions whether they are elastic or inelastic collisions there is always one thing we conserve which is momentum. If those collisions are elastic then we will conserve kinetic energy too. In case of inelastic collisions we can’t conserve the kinetic energy because it is lost in the form of heat or sound.

Formula used:
$s = ut + \dfrac{1}{2}a{t^2}$

Complete answer:
According to Newton's second law as long as there is no external impulsive force momentum will always be conserved. For example if a bomb or rock explodes then we can conserve the momentum because explosion is considered as an internal reaction. So when there is no external impulsive force we find out the momentum of the rock or bomb before it gets exploded and we equate it to the momentum of the system of pieces after the rock had exploded. In this we solve many problems.
By considering ball and floor as one system we conserve momentum too.
Since it is rebounding to the same height, the collision is elastic and the velocity of the ball before collision is the same as the velocity after collision. Initial velocity of the ball is zero. We have kinematic equation
$s = ut + \dfrac{1}{2}a{t^2}$
Here ‘s’ is measured from the point of dropping. From ground distance(H) will be total height minus ‘s’ i.e $H = 2 - s$
$\eqalign{
  & s = ut + \dfrac{1}{2}a{t^2} \cr
  & \Rightarrow s = 0 + \dfrac{1}{2}g{t^2} \cr
  & \Rightarrow H = 2 - s \cr
  & \Rightarrow H = 2 - \dfrac{1}{2}g{t^2} \cr
  & \therefore H = a - b{t^2} \cr} $
Graph for the equation $H = a - b{t^2}$ will be vertically inverted parabola. Since time cant be negative, there will be no negative portion. Below graph satisfies the required condition.

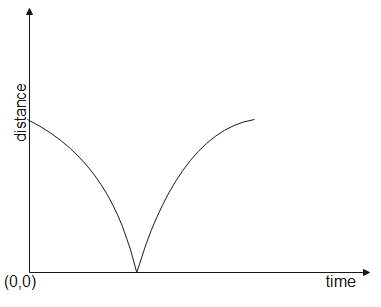
Hence option C will be the answer.

Note:
In the graphs given above, option B can never be answered because distance is negative there. Distance can never be negative. Option A is not an answer because initially the ball must be at maximum distance from ground but in the first graph it is at zero distance. Hence that cannot be an answer