Question

An ellipse has OB as semi-minor axis, F and F’ its foci and the \[\angle FBF'\] is a right angle. Then, the eccentricity of the ellipse is
(A) \[\dfrac{1}{\sqrt{3}}\]
(B) \[\dfrac{1}{4}\]
(C) \[\dfrac{1}{2}\]
(D) \[\dfrac{1}{\sqrt{2}}\]

Answer 1

Hint: Assume an ellipse with F and F’ as its foci, the length of the major and minor axes are \[a\] and
\[b\] respectively. We know the property of the ellipse that the coordinates of its foci are \[\left( -ae,0 \right)\] and \[\left( ae,0 \right)\] . In \[\Delta BOF\] and \[\Delta BOF'\] , apply the formula \[\tan \theta =\dfrac{Perpendicular}{Base}\] for \[\angle BFO\] and
\[\angle BF'O\] . Since it is given that BF and BF’ are perpendicular to each other and we know the property that the product of the slope of two perpendicular lines is -1. Now, apply this property for the lines BF and BF’, and obtain the relation between \[a\] , \[b\] , and \[e\] . At last, use the formula for the eccentricity of ellipse, \[e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}\] and calculate the value of \[e\] .

Complete step by step answer:
According to the question, we are given an ellipse that has OB as semi-minor axis, F and F’ its foci and the \[\angle FBF'\] is a right angle.
Let us assume an ellipse with F and F’ as its foci, the length of the major and minor axes are \[a\] and
\[b\] respectively …………………………………………(1)
We know the property of the ellipse that the coordinates of its foci are \[\left( -ae,0 \right)\] and \[\left( ae,0 \right)\] ……………………………………………(2)
Here, F and F’ are the foci of the given ellipse …………………………………….……(3)
Now, from equation (2) and equation (3), we get
The coordinate of the focus F = \[\left( ae,0 \right)\] ……………………………………..(4)
The coordinate of the focus F’ = \[\left( -ae,0 \right)\] ……………………………………..(5)
Now, let us draw the diagram of the ellipse for the given information.
 

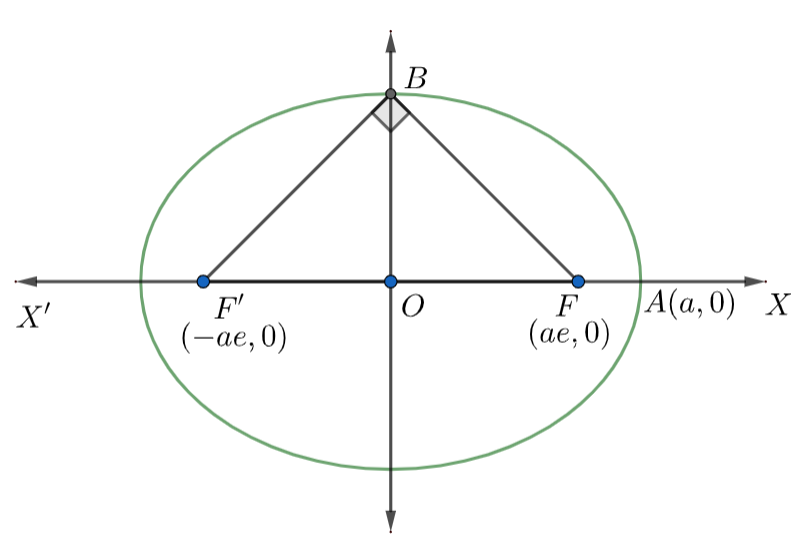
In the above diagram, we can observe that
\[\angle BFX+\angle BFO=180{}^\circ \] (linear pair)
\[\angle BFX=180{}^\circ -\angle BFO\] ……………………………………………(6)
Similarly, \[\angle BF'X+\angle BF'O=180{}^\circ \] (linear pair)
\[\angle BF'X=180{}^\circ -\angle BF'O\] ……………………………………………(7)
Now, in \[\Delta BOF\] , we have
Perpendicular = OB = \[b\] (length of minor axis) ………………………………(8)
Base = OF = \[ae\] (from the diagram) …………………………………….(9)
We also know that \[\tan \theta =\dfrac{Perpendicular}{Base}\] …………………………………..(10)
 Now, from equation (8), equation (9), and equation (10), we get
\[\tan \angle BFO=\dfrac{b}{ae}\] …………………………………………..(11)
Now, in \[\Delta BOF'\] , we have
Perpendicular = OB = \[b\] (length of minor axis) ………………………………(12)
Base = OF’ = \[ae\] (from the diagram) …………………………………….(13)
Now, from equation (10), equation (12), and equation (13), we get
\[\tan \angle BF'O=\dfrac{b}{ae}\] …………………………………………..(14)
The slope of line BF = \[\tan \angle BFX\] ………………………………………….(15)
Now, from equation (6) and equation (15), we get
The slope of line BF = \[\tan \left( 180{}^\circ -\angle BF0 \right)=-\tan \angle BFO\] ……………………………………..(16)
The slope of line BF’ = \[\tan \angle BF'X\] ………………………………………….(17)
Now, from equation (7) and equation (17), we get
The slope of line BF’ = \[\tan \angle BF'X=\tan \angle BF'O\] ……………………………………..(18)
Since it is given that BF and BF’ are perpendicular to each other and we know the property that the product of the slope of two perpendicular lines is -1 …………………………………………….(19)
Now, from equation (16), equation (18), and equation (19), we get
\[\Rightarrow \left( -\tan \angle BFO \right)\times \left( \tan \angle BF'O \right)=-1\] ……………………………………(20)
Now, from equation (11), equation (14), and equation (20), we get
 \[\begin{align}
  & \Rightarrow \left( -\dfrac{b}{ae} \right)\times \left( \dfrac{b}{ae} \right)=-1 \\
 & \Rightarrow \dfrac{{{b}^{2}}}{{{a}^{2}}{{e}^{2}}}=1 \\
\end{align}\]
\[\Rightarrow {{b}^{2}}={{a}^{2}}{{e}^{2}}\] ……………………………………..(21)
We know the formula for the eccentricity of ellipse, \[e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}\] …………………………………….(22)
Now, from equation (21) and equation (22), we get
\[\begin{align}
  & \Rightarrow e=\sqrt{1-\dfrac{{{a}^{2}}{{e}^{2}}}{{{a}^{2}}}} \\
 & \Rightarrow {{e}^{2}}=1-{{e}^{2}} \\
 & \Rightarrow 2{{e}^{2}}=1 \\
 & \Rightarrow e=\sqrt{\dfrac{1}{2}} \\
\end{align}\]
Therefore, the eccentricity of the ellipse is \[\dfrac{1}{\sqrt{2}}\] .

So, the correct answer is “Option D”.

Note: For solving this question, we have to recall three points. The first one is that the coordinates of its foci are \[\left( -ae,0 \right)\] and \[\left( ae,0 \right)\]. The second one is that the product of the slope of two perpendicular lines is -1. The third one is the formula for the eccentricity of ellipse, \[e=\sqrt{1-\dfrac{{{b}^{2}}}{{{a}^{2}}}}\].