Question

An ellipse has eccentricity \[\dfrac{1}{2}\] and one focus at the point \[P\left( {\dfrac{1}{2},1} \right)\]. Its one directrix is the common tangent, nearer to the point P, to the circle \[{x^2} + {y^2} = 1\] and hyperbola \[{x^2} - {y^2} = 1\]. Find the equation of the ellipse in standard form.

Answer 1

Hint: First, find the equation of the common tangents. Then find the unit shift of the ellipse in the conventional direction. Then, apply the formula of standard form of the equation of the ellipse. The formula of the distance between the focus and the direction shift gives the values of the variables used in standard form.

Formula Used:
The formula for the equation of the ellipse in the standard form is given by:
\[\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\]

Complete step by step answer:

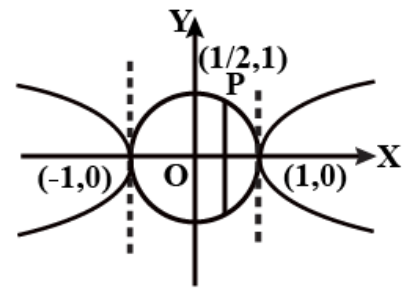
In the question, the two given equations are
\[ \Rightarrow {x^2} + {y^2} = 1\]
\[ \Rightarrow {x^2} - {y^2} = 1\]
We solve them for the value of \[x\]; add them and apply the square root and we get:
\[x = 1\] and \[x = - 1\]
Now, from the two equations, the one closer to the focus (i.e. \[P\left( {\dfrac{1}{2},1} \right)\]) is \[x = 1\].
So, a directrix of the required ellipse is \[x = 1\].
Let \[Q\left( {x,y} \right)\] be any point on the ellipse. Now, with the distance formula, its distance from the focus is:
\[QP = \sqrt {{{\left( {x - \dfrac{1}{2}} \right)}^2} + {{\left( {y - 1} \right)}^2}} \]
Then, its distance from the directrix is \[x - 1\].
Now, we know from the definition of the ellipse that
distance from focus = (eccentricity)*(distance from directrix)
Hence, we can write the formula still in the mathematical form as:
\[QP = e\left| {x - 1} \right|\]
Now, substituting the above values into the formula we get:
\[ \Rightarrow \sqrt {{{\left( {x - \dfrac{1}{2}} \right)}^2} + {{\left( {y - 1} \right)}^2}} = \dfrac{1}{2}\left( {x - 1} \right)\]
Now, squaring both sides, we have:
\[ \Rightarrow {\left( {x - \dfrac{1}{2}} \right)^2} + {\left( {y - 1} \right)^2} = \dfrac{1}{4}{\left( {x - 1} \right)^2}\]
Opening the squares and taking the \[\dfrac{1}{4}\] to the other side:
\[ \Rightarrow 4{x^2} + 1 - 4x + 4{y^2} + 4 - 8y = {x^2} + 1 - 2x\]
Now, solving the equation:
\[ \Rightarrow 3{x^2} - 2x + 4{y^2} - 8y + 4 = 0\]
Multiplying both sides by \[3\]:
\[ \Rightarrow 9{x^2} - 6x + 12{y^2} - 24y + 12 = 0\]
\[ \Rightarrow 9{x^2} - 6x + 1 + 12({y^2} - 2y + 1) = 1\]
Now, factoring the \[{x^2}\] and \[{y^2}\] separately:
\[ \Rightarrow {\left( {3x - 1} \right)^2} + 12{\left( {y - 1} \right)^2} = 1\]
Now, taking \[3\] common from the first bracket:
\[ \Rightarrow 9{\left( {x - \dfrac{1}{3}} \right)^2} + 12{\left( {y - 1} \right)^2} = 1\]
\[ \Rightarrow \dfrac{{{{\left( {x - \dfrac{1}{3}} \right)}^2}}}{{\dfrac{1}{9}}} + \dfrac{{{{\left( {y - 1} \right)}^2}}}{{\dfrac{1}{{12}}}} = 1\]
Hence, the equation of the ellipse in the standard form is:
\[ \Rightarrow \dfrac{{{{\left( {x - \dfrac{1}{3}} \right)}^2}}}{{\dfrac{1}{9}}} + \dfrac{{{{\left( {y - 1} \right)}^2}}}{{\dfrac{1}{{12}}}} = 1\]

Note: We saw in solving questions like these, it is absolutely crucial that we know all the required formulae in their standard form. These formulae are the ones which help us get out of the problem. And it is equally important that we know how to identify the formulae to be used in the equation and we know what values to use and when to use.