Question

An electron performs circular motion of radius r, perpendicular to a uniform magnetic field B. The kinetic energy gained by this electron in one revolution is_____
A. \[\dfrac{1}{2}M{{V}^{2}}\]
B. zero
C. \[\dfrac{1}{4}M{{V}^{2}}\]
D. \[\pi rBeV\]

Answer 1

Hint:When an electron or any charged particle performs circular motion, then magnetic force acts perpendicular to the particle and the kinetic energy of the electron will not change. The magnetic force acting on the body will be equal to the centrifugal force as the body moves in a circular motion.

Complete answer:
A diagram can be illustrated as follows:

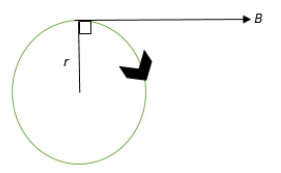
The electron performs circular motion of radius r. Also it is perpendicular to a uniform magnetic Field ‘B’.
Since, the electron moves in a direction perpendicular to the magnetic field, there is no work done, so the kinetic energy and speed of a charged particle in a uniform magnetic field remains constant.
The Centripetal force to the electron is provided by magnetic Lorentzian force so that
\[\Rightarrow qvB=\dfrac{M{{V}^{2}}}{r}\]
In general \[{{F}_{c}}=\dfrac{M{{V}^{2}}}{r}\]
So we can write ${{F}_{c}}=qvB$
The electron moves in circular motion which is perpendicular to the magnetic field. So, the kinetic energy will be zero.
\[r=\dfrac{M{{V}^{2}}}{qVB}\]
Here, r called the cyclotron radius.

Hence, the correct choice is option (B) zero.

Note:
As we know at the time of circular motion when the velocity of an electron is perpendicular to the magnetic field, the speed and kinetic energy of the particle does not change, in other words, remains constant. Also radius of circular path followed by electron is proportional to speed of electron.