Question

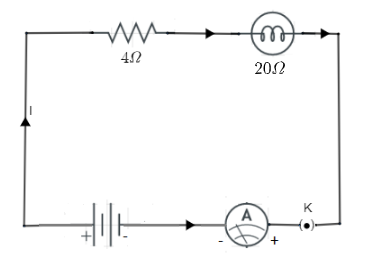
An electric lamp of the resistance 20Ω and a conductor of the resistance 4Ω are connected to a 6V battery as shown in the circuit calculate:
(A) The total resistance of the circuit
(B) The current through the circuit
(C) The potential difference across the (i) electric lamp and (ii) conductor and
(D) Power of the lamp

Answer 1

Hint: First we have to calculate resistance using the series rule and using total resistance we can calculate total current in the circuit and by using value of the current we can calculate potential difference across the electrical lamp and the conductor and we can calculate power using total current in the circuit and the voltage.

Formula used:
$\begin{align}
  & I=\dfrac{V}{R} \\
 & P=\dfrac{V}{I} \\
\end{align}$

Complete step by step solution:

(A) The total resistance of the circuit:
As we can see in the circuit that electric lamp with the resistance 20Ω and the conductor 4Ω are connected in the series, So that we can apply series rule of resistance.
Now total resistance of the circuit:
$\begin{align}
  & R=20+4 \\
 & R=24\Omega \\
\end{align}$

Hence the total resistance of the circuit is 24Ω.

(b) The current through the circuit:
We know that formula for the current (I) :
$\Rightarrow I=\dfrac{V}{R}....\left( 1 \right)$
Where, I = current
V = Voltage applied
R = total resistance
Here voltage is given as,
V = 6V
And the total resistance
R = 24Ω
Now current,
$\begin{align}
  & I=\dfrac{6}{24} \\
 & \therefore I=0.25A \\
\end{align}$
Hence current through the circuit is 0.25A.

(c) The potential difference across the
(i) Electric lamp.
If the potential difference across the electric lamp is Ve and the resistance of the electric lamp Re then,
$\begin{align}
  & \Rightarrow Ve=I\times \operatorname{Re} \\
 & \Rightarrow Ve=0.25\times 20 \\
 & \therefore Ve=5V \\
\end{align}$
Hence the potential difference across the electric lamp is 5V.
(ii) The potential difference across the conductor.
If the potential difference across the conductor is Vc and resistance of the conductor is Rc then,
$\begin{align}
  & \Rightarrow Vc=I\times Rc \\
 & \Rightarrow Vc=0.25\times 4 \\
 & \therefore Vc=1V \\
\end{align}$

(D) Power of the lamp:
Formula for the power,
\[P\text{ }=\text{ }\dfrac{\text{voltage across the lamp }\left( \text{Ve} \right)}{\text{current through lamp (I)}}\]
Where, P is power
$\begin{align}
  & \Rightarrow P=\dfrac{5}{0.25} \\
 & \therefore P=20W \\
\end{align}$

Note:
Here in the option (d) when we calculate power of the lamp don’t put the voltage as the total applied voltage instead of the voltage across the lamp (Ve) that we find in the option (c).