Question

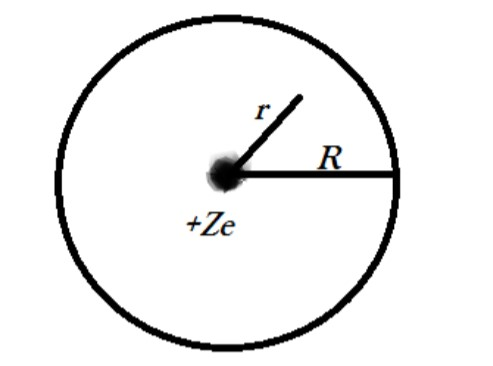
An early model for an atom considered it to have a positive charged point nucleus of charge Ze, surrounded by a uniform density of negative charge upto a radius R. The atom as a whole is neutral. The electric field at a distance r from the nucleus is (r < R)

A. $ \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{r^2}}} - \dfrac{r}{{{R^3}}}} \right] $
B. $ \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{r^2}}} - \dfrac{r}{{{R^2}}}} \right] $
C. $ \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{R^3}}} - \dfrac{r}{{{R^2}}}} \right] $
D. $ \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{R^3}}} + \dfrac{r}{{{r^2}}}} \right] $

Answer 1

Hint: Gauss’s law, also known as Gauss’s flux theorem, is a law relating the distribution of electric charge to the resulting electric field. The surface under consideration may be a closed one enclosing a volume such as a spherical surface.

Complete step by step solution:
The net electric flux through any hypothetical closed surface is equal to $ \dfrac{1}{{\varepsilon o}}$ times the net electric charge within that closed surface.
According to the question we have to find the electric field at a distance r from the nucleus.
Charge on nucleus is $ = + Ze $
Total negative charge is $ = - Ze $
$ \therefore $ Negative charge density
$
\rho = \dfrac{{ch\arg e}}{{volume}} = \dfrac{{ - Ze}}{{\dfrac{4}{3}\pi {R^3}}} \\

\therefore \Rightarrow \rho = - \dfrac{{3Ze}}{{4\pi {R^3}}} \\
 $
So applying gauss law and making the Gaussian surface of radius r
$ \therefore $ According to gauss law,
$ \oint {E.dA = \dfrac{{q(enclosed)}}{{\varepsilon o}}} $
Here the area will be the area enclosed by Gaussian surface and q will be the charge enclosed within the Gaussian surface.
$ \because $ charge per unit volume is $ \rho = - \dfrac{{3Ze}}{{4\pi {R^3}}} $
$ \therefore $ charge enclosed within the Gaussian surface of radius r
$
= \dfrac{4}{3}\pi {r^3} \times - \dfrac{{3Ze}}{{4\pi {R^3}}} \\
= \dfrac{{ - Ze{r^3}}}{{{R^3}}} \\
 $
Thus charge enclosed within the Gaussian surface of radius r = $ \dfrac{{ - Ze{r^3}}}{{{R^3}}} $
Now,
According to gauss law,
\[
\oint {E.dA = \dfrac{{q(enclosed)}}{{\varepsilon o}}} \\
\therefore this \Rightarrow E.4\pi {r^2} = \dfrac{{q(enclosed)}}{{\varepsilon o}} \\
\Rightarrow E.4\pi {r^2} = \dfrac{{ + Ze + (\dfrac{{ - Ze{r^3}}}{{{R^3}}})}}{{\varepsilon o}} \\
\Rightarrow E = \dfrac{1}{{4\pi {r^2}\varepsilon o}}\left[ {Ze - \dfrac{{Ze{r^3}}}{{{R^3}}}}
\right] \\
\Rightarrow E = \dfrac{{Ze}}{{4\pi {r^2}\varepsilon o}}\left[ {1 - \dfrac{{{r^3}}}{{{R^3}}}} \right]
\\
\Rightarrow E = \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{r^2}}} -
\dfrac{{{r^3}}}{{{r^2} \times {R^3}}}} \right] \\
\Rightarrow E = \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{r^2}}} - \dfrac{r}{{{R^3}}}}
\right] \\
\]
Thus the required electric field is \[E = \dfrac{{Ze}}{{4\pi \varepsilon o}}\left[ {\dfrac{1}{{{r^2}}} -
\dfrac{r}{{{R^3}}}} \right]\]

Note: In order to solve these types of questions always choose the Gaussian surface wisely such that it can make your calculations easy and find the area of the surface and the charges accordingly.