Question

An eagle is flying at a constant height of $1000\sqrt 3 $ m from the ground level. A boy standing on the ground observes the angle of elevation of the eagle ${45^\circ}$. After a flight of 15 seconds its angle of elevation at the same period is observed to be ${30^\circ}$. Find the speed of the eagle in km/h.

Answer 1

Hint: First we need to find the distance travelled by the eagle in 15 seconds time. Then we have to apply different trigonometric functions in triangles in the diagram created. Then proper substitution of the values and some calculations we will find the result. Also we have to convert the result in the required unit as given in the question.

Complete step-by-step answer:
First we will draw the essential diagram. It will show the two positions of eagle and both angles of elevation of the eagle by the boy, who is static at his place. Also, height of eagle and speed both will be constant.
          

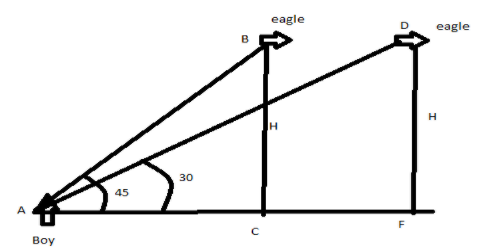
We need the help of trigonometric and formulas of velocity.
$v = \dfrac{s}{t}$
where v is the velocity, s is distance and t time.
Given data in the question,
t = 15 s
Height of eagle $ = BC = DF = 1000\sqrt 3 m$
$\angle BAC = {45^\circ }$, $\angle DAF = {30^\circ }$
In triangle ABC we have,
$\tan \angle BAC = \dfrac{{perpendicular}}{{base}}$
Putting the values, we have
$\therefore \tan \angle BAC = \dfrac{{BC}}{{AC}}$
$ \Rightarrow \tan {45^\circ } = \dfrac{{1000\sqrt 3 }}{{AC}}$
$ \Rightarrow AC = 1000\sqrt 3 $
And further in triangle DAF we have,
$\tan \angle DAF = \dfrac{{perpendicular}}{{base}}$
Putting the values, we have
$\tan \angle DAF = \dfrac{{DF}}{{AF}}$
$ \Rightarrow \tan {30^\circ } = \dfrac{{1000\sqrt 3 }}{{AF}}$
$ \Rightarrow AF = \dfrac{{1000\sqrt 3 }}{{1/\sqrt 3 }}$
$ \Rightarrow AF = 3000 m$
The eagle travelled distance from C to F position, so distance CF will be,
$\therefore CF = 3000 - 1000\sqrt 3 $
We know that the formula for speed, $speed = \dfrac{{distance}}{{time}}$
$\therefore v = \dfrac{{3000 - 1000\sqrt 3 }}{{15}}$
Solving above equation, we get
$ = 84.52 m/s$
$\therefore $ The speed of eagle in km/h (conversion needed)
To convert the speed we have to multiply the speed by 1000 and further divided by 3600 ($60 \times 60$).
So, doing this we get,
$
   = \dfrac{{84.52 \times 1000}}{{60 \times 60}} \\
   = 23.48km/h \\
 $
The speed of the eagle was 23.48 km/h.

Note: In this type of math problem we need a good visualization of the given situation. And also suitable use of formulas of trigonometric and some other needed formulas as here we need speed distance formula. Trigonometric equations & their values should be written carefully to avoid the calculative error.