Question

An annular disc of inner radius a and outer radius \['2a'\] is uniformly charged with uniform surface charge density \[\sigma \]. Find the potential at a distance \['a'\] from the centre at a point lying on the axis.

     

Answer 1

Hint:In order to calculate the potential at a distance from the centre at a point lying on the axis, we need to draw a figure as below to get points clearly.

Complete step-by-step answer:
     

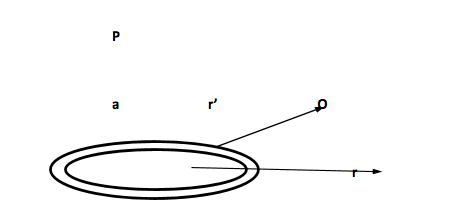
The charge contained in the elementary ring,
\[dq = \sigma (2\pi rdr)\]
The potential due to the ring at P,
\[ = dV = \dfrac{{dq}}{{4\pi {\varepsilon _0}r\prime }}\]
The total potential at P due to the given disc V,
\[ = \smallint dV = \dfrac{1}{{4\pi {\varepsilon _0}}}\smallint \dfrac{{dq}}{r}\]
Since, \[dq = \sigma 2\pi rdr\] and \[r\prime = \sqrt {{a^2} + {r^2}} \]
\[ \Rightarrow {V_p} = \dfrac{\sigma }{{2{\varepsilon _0}}}[\sqrt {{a^2} + {r^2}} ]_{r = a}^{r = 2a} = \dfrac{\sigma }{{2{\varepsilon _0}}}a(\sqrt 5 - \sqrt 2 )\]
Thus, the answer to this question is \[\dfrac{\sigma }{{2{\varepsilon _0}}}a(\sqrt 5 - \sqrt 2 )\].

Additional Information: When the charge is uniformly distributed over the surface of the conductor, it is called Surface Charge Density or Surface Charge Distribution. It is denoted by the symbol \[{\mathbf{\sigma }}\] (sigma) symbol and the unit is \[C/{m^2}\]. It is also defined as charge/ per unit area. Mathematically surface charge density is \[{\mathbf{\sigma }} = \dfrac{{dq}}{{ds}}\] where \[dq\] is the small charge element over the small surface ds. So, the small charge on the conductor will be $dq = \sigma ds$.

Note:While solving this question, we should be aware of the different types of formula used here. Especially surface charge density and how the different values of the variable of the formula is used from the question. The formula is modified and used here to take out the required solution for the problem given here. Different formulae is used here which must be taken into consideration while solving the question.