Question

An airplane is flying at a height of 300m above the ground. Flying at this height, the angles of depression from the airplane of two points on both the banks of a river in the opposite directions are \[{{45}^{o}}\] and \[{{60}^{o}}\] respectively. Find the width of the river. [Use \[\sqrt{3}=1.732\]]

Answer 1

Hint: To solve this question, we have to visualize the given condition and then we will apply the values of the trigonometric ratios to find the width of the river. Also, we should know that the angle of depression is the angle between the axis of the plane and the line joining the plane to the bank of the river.

Complete step-by-step answer:
In this question, we have to find the width of the river when it is given that the angle of depression on both the banks of the river, from the airplane flying at a height of 300m is \[{{45}^{o}}\] and \[{{60}^{o}}\] respectively.

Now, from the given condition, we can say that the diagram will look something like this;

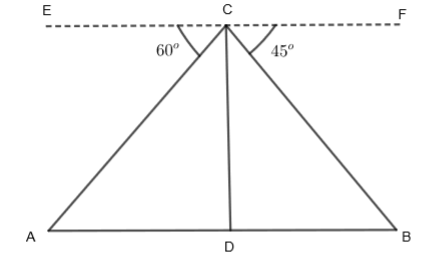
From the alternate angle property, we can say that \[\angle ECA=\angle CAD={{60}^{o}}\] and \[\angle FCB=\angle CBD={{45}^{o}}\]. Now, we know that the tangent ratio of an angle is the ratio of the perpendicular to the base. Therefore, we can write,
\[\tan \angle CAD=\dfrac{CD}{AD}\]
Now, we know that \[\angle CAD={{60}^{o}}\] and CD = 300m. So, we can write,
\[\tan {{60}^{o}}=\dfrac{300}{AD}\]
Now, we know that \[\tan {{60}^{o}}=\sqrt{3}\]. So, we can write,
\[\sqrt{3}=\dfrac{300}{AD}\]
\[AD=\dfrac{300}{\sqrt{3}}\]
\[AD=\dfrac{3\times 100}{\sqrt{3}}\]
\[AD=100\times \sqrt{3}\]
Now, in the question, we are asked to use \[\sqrt{3}=1.732\]. Therefore, we can write
\[AD=100\times \left( 1.732 \right)\]
\[AD=173.2m.....\left( i \right)\]
Now, we will write the tangent ratio for the angle CBD. So, we will get,
\[\tan \angle CBD=\dfrac{CD}{DB}\]
Now, we know that \[\angle CBD={{45}^{o}}\] and CD = 300m. So, we will get,
\[\tan {{45}^{o}}=\dfrac{300}{DB}\]
Now, we know that \[\tan {{45}^{o}}=1\]. Therefore, we will get
\[1=\dfrac{300}{DB}\]
\[DB=\dfrac{300}{1}\]
\[DB=300m....\left( ii \right)\]
Now, we know that the width of the river is AB which is equal to the sum of AD and DB. Therefore, we can write it as
AB = AD + DB
Now, we will put the values of AD and DB from equation (i) and (ii). So, we will get,
AB = 173.2 + 300
AB = 473.2m
Hence, we can say that the width of the river is 473.2m.

Note: In a hurry, the possible mistake one can make is by considering both the angle of depression in one direction which will give you the wrong answer. Also, we may make a mistake while writing the values of \[\tan {{60}^{o}}\] and \[\tan {{45}^{o}}\] which is equal to \[\sqrt{3}\] and 1 respectively.