Question

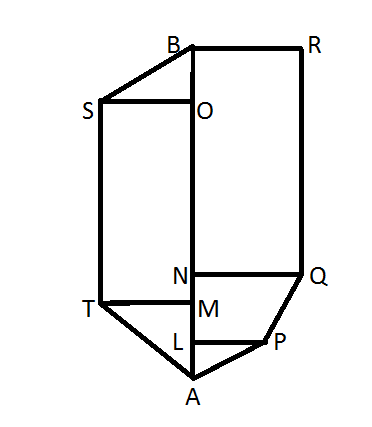
An agriculture field has a shape of an irregular polygon as shown in the figure. Its dimensions are given so find the area.
Given: AB = 220m, AL = 20m, AM = 30m, BN = 160m, OB = 40m, TM = OS = 60m, LP = 20m, NQ = 60m, MN = 30m.

Answer 1

Hint: In order to solve this problem we need to calculate the area of every divided part with the help of lengths given and then add all of them to get the value of the area. We will be getting the figure of right angled triangles, rectangles and trapezium and the area of right angled triangle is half of base multiplied by height, area of rectangle is length multiplied by breadth and area of trapezium is altitude multiplied by sum of parallel sides.

Complete step-by-step answer:
It is given that AB = 220m, AL = 20m, AM = 30m, BN = 160m, OB = 40m, TM = OS = 60m, LP = 20m, NQ = 60m, MN = 30m.
First we calculate the area of the right angled triangle BOS.
We have OS = 60m.
OB = 40m.
Therefore the area will be $\dfrac{{\text{1}}}{{\text{2}}}{base \times height}$.
$\dfrac{{\text{1}}}{{\text{2}}}{{60 \times 40 = 1200}}{{\text{m}}^2}$…………(1)
Now area of rectangle BRQN.
NQ = 60, BN = 160m
Area = 60 x 160 =${\text{9600}}{{\text{m}}^{\text{2}}}$……………(2)
Now we will find the area of trapezium LPNQ.
Area of trapezium LPNQ = $\dfrac{{\text{1}}}{{\text{2}}}{\text{(NQ + LP)NL}}$
MN = AM – AL = 10m.
NL = MN +ML = 30 + 10 = 40m
So, area = $\dfrac{{\text{1}}}{{\text{2}}}{\text{(20 + 60)40 = 3200}}{{\text{m}}^2}$……….(3)
Now area of rectangle SOTM = OM x OS
OM = AB – OB – AM = 220 – 40 – 30 = 150m
So, the area of SOTM will be OM x OS = 150 x 60 = $9000{m^2}$…….(4)
Now the area of triangle TMA = $\dfrac{{\text{1}}}{{\text{2}}}{\text{(TN)(AM)}}$ .
Area = $\dfrac{{\text{1}}}{{\text{2}}}{\text{(30)(60) = 30x30 = 900}}{{\text{m}}^2}$…………………(5)
Now the area of triangle ALP = $\dfrac{{\text{1}}}{{\text{2}}}{\text{(AL)(LP)}}$.
Area = $\dfrac{1}{2}(20)(20) = 200{m^2}$………..(6)
Hence the area of the field will be the sum of all the areas we have calculated above. So we do,
1200 + 9600 + 3200 + 9000 + 900 + 200 = 24100 square meter will be the area of the required field.

Note: In order to get this problem right we need to remember the area of various figures like triangles, rectangles squares, triangles and trapezium. Knowing these will solve most of the problems and will give you the right answers.