Question

An aeroplane when 3000 m high, passes vertically above another aeroplane at an instant when the angles of elevation of the two aeroplanes from the same point on the ground are ${{60}^{\circ }}$and ${{45}^{\circ }}$respectively. Find the vertical distance between the two planes.

Answer 1

Hint: First, before proceeding for this, we must draw the diagram of the condition in which the plane above the another plane is 3000m and let us suppose the height of the place closer to ground as x. Then, applying the trigonometric identity in the triangle ADC, we get the value of the base. Then, we will use the same condition for the triangle BDC and get the value of x and then we get the desired result after subtraction.

Complete step-by-step answer:
In this question, we are supposed to find the vertical distance between the two planes which are flying over one another and the angles of elevation from the point on the ground are ${{60}^{\circ }}$and ${{45}^{\circ }}$respectively.
So, before proceeding for this, we must draw the diagram of the condition in which the plane above the another plane is 3000m and let us suppose the height of the plane closer to ground as x.
So, the figure will look like:

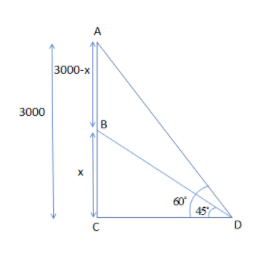
Now, we will recall that the aeroplane at a height of 3000m at point A passes over another aeroplane at B at height x metres.
So, we can get the angle of elevation of higher aeroplane from the figure as:
$\angle ADC={{60}^{\circ }}$
Similarly, the angle of elevation of lower aeroplane from the figure as:
$\angle BDC={{45}^{\circ }}$
Now, by applying the trigonometric identity in the triangle ADC, we get:
$\tan {{60}^{\circ }}=\dfrac{AC}{DC}$
Then, by substituting the value of AC as 3000 and calculate for DC, we get:
$\begin{align}
  & \sqrt{3}=\dfrac{3000}{DC} \\
 & \Rightarrow DC=\dfrac{3000}{\sqrt{3}} \\
 & \Rightarrow DC\approx 1732 \\
\end{align}$
So, we get the value of base DC as 1732 metres.
Now, we will use the same condition for the triangle BDC and get the value of x as:
$\tan {{45}^{\circ }}=\dfrac{BC}{DC}$
Then, by substituting the value of BC as x and DC as 1732 as calculated above, we get:
$\begin{align}
  & 1=\dfrac{x}{1732} \\
 & \Rightarrow x=1732 \\
\end{align}$
So, we get the value of x as 1732 metres.
Then, we need the value of difference in the height of the aeroplanes which is given by:
$\begin{align}
  & 3000-x=3000-1732 \\
 & \Rightarrow 1268 \\
\end{align}$
So, the vertical distance between the two planes is 1268m.
Hence, 1268m is the answer.

Note: Now, to solve these type of the questions we need to know some of the basics of designing the figure from the given data as in this question two aeroplanes are flying one over the another and a point on the ground is considered to get two angles as imagine you are at one point the two aeroplanes are flying one at height h and other at height 2h gives two different angles of elevation from same point. So, our imagination power should be strong to solve these kinds of problems.