Question

An aeroplane is flying horizontally at a height of 3150 m above a horizontal plane ground. At a particular instant, it passes another plane vertically below it. At this instant, the angles of elevation of the planes from a point on the ground are ${30^0}$ and ${60^0}$. Hence, the distance between the two planes at that instant is
A. 1050 m
B. 2100 m
C. 4200 m
D. 5250 m

Answer 1

Hint: Start with drawing a figure from the given information in the question, once the diagram is drawn you can apply trigonometric ratios in two triangles formed to get the required distances that is find the height of the second plane and subtract that from the height of the first plane.

Complete step-by-step answer:

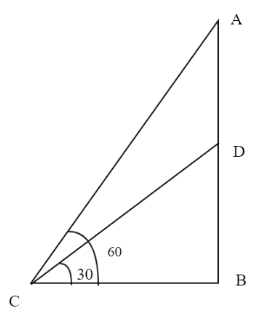
Now, in the figure, AB = 3150 m. At, B there is another plane. Let the distance between two planes be x. So, AD = x m. So, BD = 3150 – x m. Now, we will use tan x and value of tan x at ${30^0}$ and ${60^0}$.
Now, in triangle ABC,
\[\tan {\text{ 6}}{{\text{0}}^0}{\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{BC}}}}\]
Now, we know that \[\tan {\text{ 6}}{{\text{0}}^0}{\text{ = }}\sqrt 3 \]. So,
\[\sqrt 3 {\text{ = }}\dfrac{{3150}}{{{\text{BC}}}}\]
Therefore, BC = $\dfrac{{3150}}{{\sqrt 3 }}$ m … (1)
Now, in triangle BCD,
$\tan {\text{ 3}}{{\text{0}}^0}{\text{ = }}\dfrac{{{\text{BD}}}}{{{\text{BC}}}}$
As, $\tan {\text{ 3}}{{\text{0}}^0}{\text{ = }}\dfrac{1}{{\sqrt 3 }}$
So, $\dfrac{1}{{\sqrt 3 }}{\text{ = }}\dfrac{{3150{\text{ - x}}}}{{{\text{BC}}}}$
Therefore, BC = $\sqrt 3 (3150{\text{ - x)}}$ m
Now, from equation (1) comparing value of BC, we get
$\dfrac{{3150}}{{\sqrt 3 }}{\text{ = }}\sqrt 3 (3150{\text{ - x)}}$
Solving the above equation, we get
3150 = 3(3150 – x)
3150 = 9450 – 3x
3x = 6300
x = 2100 m
So, the distance between two planes = x m = 2100 m
So, option (B) is correct.

Note: When we come up with such types of questions, the easiest way to solve the question is by using trigonometric ratios and their values at few angles. We have to follow a few steps to solve the given problem. We will first let the value be x and then we will apply trigonometric ratios in each triangle to find the value of x. Figure plays a very important role in solving such problems, so it is necessary to draw a figure to get a correct answer.