Question

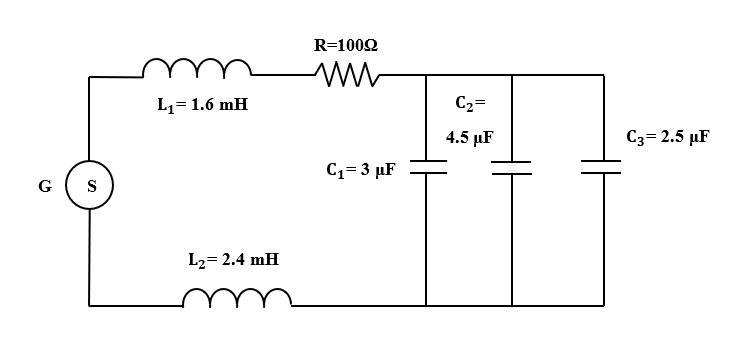
An ac generator G with an adjustable frequency of oscillation is used in the circuit, as shown. Current drawn from the ac source will be maximum if its angular frequency is

$A. { 10 }^{ 5 }{ rad }/{ s }$
$B. { 10 }^{ 4}{ rad }/{ s }$
$C. 5000{ rad }/{ s }$
$D. 500{ rad }/{ s }$

Answer 1

Hint: To solve this problem, first find the equivalent capacitance of the combination of three capacitors which are connected in series. Then, find the equivalent inductance of a combination of inductors which are connected in series. Now, use the formula for angular frequency in terms of equivalent capacitance and equivalent inductance. Substitute the values in the formula and find the angular frequency when the current drawn from the ac source is maximum.
Formula used:
${C}_{eq}= {C}_{1}+ {C}_{2} + {C}_{3}$
${L}_{eq}={L}_{1}+ {L}_{2}$
$\omega= \dfrac {1}{\sqrt {LC}}$

Complete answer:
Given: ${L}_{1}= 1.6 mH$
            ${L}_{2}= 2.4 mH$
            ${C}_{1}= 3 \mu H$
            ${C}_{2}= 4.5 \mu H$
            ${C}_{3}= 2.5 \mu H$
            $R= 100 \Omega$
All the three capacitors are connected in parallel. So, their equivalent capacitance is given by,
${C}_{eq}= {C}_{1}+ {C}_{2} + {C}_{3}$
Substituting values in above equation we get,
${C}_{eq}= 3 + 4.5 + 2.5$
$\Rightarrow {C}_{eq}= 10 \mu F$
Both the inductors are connected in series. So, their equivalent inductance is given by,
${L}_{eq}={L}_{1}+ {L}_{2}$
Substituting values in above equation we get,
${L}_{eq}= 1.6 + 2.4$
$\Rightarrow {L}_{eq}= 4 mH$
At resonance, angular frequency is given by,
$\omega= \dfrac {1}{\sqrt {LC}}$
$\Rightarrow \omega= \dfrac {1}{\sqrt {{L}_{eq}{C}_{eq}}}$
Substituting values in above equation we get,
$\omega =\dfrac { 1 }{ \sqrt { 4\times { 10 }^{ -3 }\times 10\times { 10 }^{ -6 } } }$
$\Rightarrow \omega =\cfrac { 1 }{ \sqrt { 40\times { 10 }^{ -9 } } }$
$\Rightarrow \omega =\cfrac { 1 }{ 2\times { 10 }^{ -4 } }$
$\Rightarrow \omega= 0.5 \times {10}^{4}$
$\Rightarrow \omega= 5000 Hz$
$\Rightarrow \omega= 5000 { rad }/{ s }$
Thus, Current drawn from the ac source will be maximum if its angular frequency is $5000 { rad }/{ s }$.

So, the correct answer is option C i.e. $5000 { rad }/{ s }$.

Note:
Students must remember that when the capacitors are connected in series, the total capacitance is less than at least any one of the series capacitors individual capacitance. When capacitors are connected in parallel, the total capacitance is the sum of all the capacitors’ capacitances. The equivalent inductance of any two or more inductors connected together in series will always be greater than the value of the largest inductor in the series chain.