Question

AM is a median of a triangle ABC. Is AB+BC+CA> 2AM?
(Consider the sides of triangles ABM and AMC)

Answer 1

Hint: We will use inequalities of the triangle that the sum of any two sides of a triangle is greater than or equal to the third side. We will divide the triangle into two parts and then apply the inequality in each sub triangle.

Complete step-by-step answer:

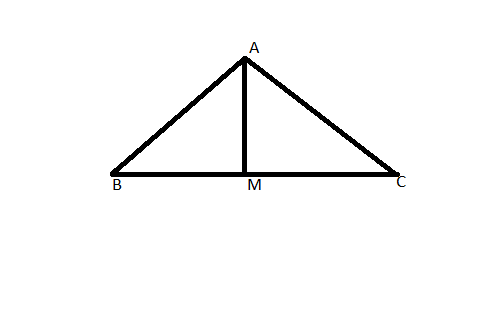
We are given a triangle ABC and AM is median on the side BC.
We can prove AB+BC+CA> 2AM by starting with the triangles.
So, in the triangle ABC. We have sub triangles ABM and AMC.
So, in triangle ABM
Using the inequality of the triangle that the sum of any two sides is always greater than or equal to the third side.
We have $AB+BM>AM$. …………………… (1)
Also using the same in triangle AMC,
We have $AC+MC>AM$. ……………………. (2)
Adding equation (1) and (2), We get
$AB+AC+(BM+MC)>2AM$
=$AB+AC+BC>2AM$
Hence AB+BC+CA>2AM is proved to be true.

Note: The proof is valid in general even if AM is not the median of the triangle. In the solution, we haven’t made use of the median AM as given in the problem. We used the triangle inequality in the $\vartriangle $ABM and $\vartriangle $AMC and used the inequalities that sum of any two sides is greater than or equal to the third side which is valid always even when we have not been given that AM is median.