Question

Altitude on the hypotenuse of a right-angled triangle divides it in two parts of lengths $4cm$ and $9cm$. Find the length of the altitude.
$A)9cm$
$B)4cm$
$C)6cm$
$D)2\sqrt 6 cm$

Answer 1

Hint: First we have to define what the terms we need to solve the problem are.
A triangle in which one of the interior angles is \[90^\circ \] is called a right triangle.
It is given that the hypotenuse exceeds from both base and altitude. So, we will get two values of hypotenuse, we can use Pythagoras theorem to establish the right-angled triangle.

Complete step by step answer:

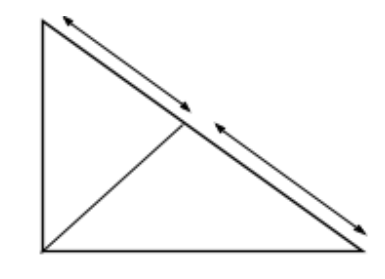
Since it is given that altitude on the hypotenuse of a right-angled triangle divides it in two parts of lengths $4cm$and $9cm$.
So, we just take $AC$and its midpoint is $D$and then it divides two parts with lengths $4cm$and $9cm$.
In these questions we need to be vary fare full at putting the values as base and perpendicular, hypotenuse too,
Clearly, we see that $\vartriangle DAB \sim \vartriangle DBC$
So that $\dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{BD}}$and Pythagoras theorem which states that ${(Hpy)^2} = {(Base)^2} + {(altitude)^2}$in the right angled and hence we get $B{D^2} = DC \times AD$
Thus we need to find the value of $BD$which is the altitude of the given problem needed to establish so apply the known values $DC$and $AD$which are $4cm$ and $9cm$ respectively.
Hence, we get $B{D^2} = DC \times AD = (4 \times 9)cm$ (multiply four times of nine)
$B{D^2} = DC \times AD = (4 \times 9)cm = 36cm$ thus, we get $B{D^2} = 36cm$
Now taking roots on both sides we get $BD = \sqrt {36} cm = 6cm$
Therefore, the length of the altitude of the given right-angled triangle is $BD = 6cm$
(there is no other of getting values like $9,4,2\sqrt 6 cm$ unless calculation mistakes or applying wrong formulas)

So, the correct answer is “Option C”.

Note: For solving these types of question remember one thing which is Pythagoras theorem
Pythagoras theorem which states that ${(Hpy)^2} = {(Base)^2} + {(altitude)^2}$
And according to the questions a right-angled triangle divides it in two parts of lengths $4cm$ and $9cm$
Are the known values.