Question

All the three sides of the right triangle are integers and one side has a length of 11 units. The area of a triangle in sq. units lies between:
(a) 1 and 100
(b) 100 and 200
(c) 200 and 300
(d) More than 300

Answer 1

Hint: It is given in the question that all sides of the right triangle are integers and one of the sides is given as 11 units then from the remaining unknown two sides, let us assume that the sides are equal to x units and y units but we have to take two cases when the side 11 is the hypotenuse and when the side 11 is not the hypotenuse and then apply Pythagoras theorem in both the cases which is equal to:${{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Perpendicular \right)}^{2}}$. After applying the Pythagoras theorem, find the values of x and y. After getting the value of x and y then find the area of the triangle which is equal to one half of the multiplication of base and height of the right triangle.

Complete step-by-step solution:
We have given a right triangle in which all its sides are integer and one of its sides is given as 11 units. Let us assume the remaining sides as x and y units.
In the below figure, we have drawn a right triangle ABC.

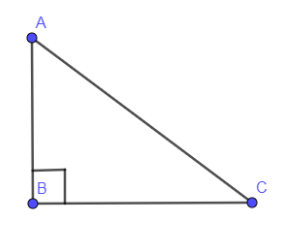
In the above figure, AC is the hypotenuse, BC is the base and AB is the perpendicular with respect to angle C.
Now, we don’t know whether 11 is hypotenuse or not so we are taking two cases when side having the length as 11 is the hypotenuse and when it is not the hypotenuse.
Case 1: When the side of length 11 units is a hypotenuse.
Then applying Pythagoras theorem on sides of length 11, x and y we get,
A Pythagoras theorem states that the square of the hypotenuse is equal to the sum of the square of the base and the perpendicular which we have shown below mathematically.
${{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Perpendicular \right)}^{2}}$
Substituting hypotenuse as 11, base and perpendicular as x and y respectively in the above equation we get,
$\begin{align}
  & {{\left( 11 \right)}^{2}}={{\left( x \right)}^{2}}+{{\left( y \right)}^{2}} \\
 & \Rightarrow 121={{\left( x \right)}^{2}}+{{\left( y \right)}^{2}} \\
\end{align}$
The values that ${{x}^{2}}\And {{y}^{2}}$ can take is equal to:
$1,4,3,16,25,36,49,64,81,100$
But if we use these values in the above equation then none of the values can satisfy the above equation.
Hence, in this case, we are getting no values of x and y.
Case 2: When 11 is not the hypotenuse then we can take x or y any one of them as the hypotenuse.
We are taking x as the hypotenuse in the Pythagoras theorem we get,
$\begin{align}
  & {{\left( x \right)}^{2}}={{\left( 11 \right)}^{2}}+{{\left( y \right)}^{2}} \\
 & \Rightarrow {{\left( x \right)}^{2}}=121+{{\left( y \right)}^{2}} \\
\end{align}$
Subtracting ${{y}^{2}}$ on both the sides of the above equation we get,
${{x}^{2}}-{{y}^{2}}=121$
We know, there is an identity in the algebra which is equal to:
$\left( x+y \right)\left( x-y \right)=121$
We know there are two ways in which we can write 121 which are:
$\begin{align}
  & 11\times 11 \\
 & 121\times 1 \\
\end{align}$
As the factors written on the left hand side of the above equation is also two factors which are written with a multiplication sign so we can equate those two factors in x and y to the above factors we get,
$\begin{align}
  & x+y=11..........Eq.(1) \\
 & x-y=11..........Eq.(2) \\
\end{align}$
Adding the above two equations we get,
$\begin{align}
  & 2x=22 \\
 & \Rightarrow x=11 \\
\end{align}$
Now, substituting the above value of x in eq. (1) we get,
$\begin{align}
  & 11+y=11 \\
 & \Rightarrow y=0 \\
\end{align}$
In the above solution, we are getting y as 0 and the side of a triangle cannot be 0 so this solution of x and y could not be possible.
Now, taking the second case $121\times 1$ we get,
$\begin{align}
  & x+y=121........Eq.(3) \\
 & x-y=1..........Eq.(4) \\
\end{align}$
Adding the above two equations we get,
$\begin{align}
  & 2x=122 \\
 & \Rightarrow x=61 \\
\end{align}$
Substituting the above value of x in eq. (3) we get,
$\begin{align}
  & 61+y=121 \\
 & \Rightarrow y=121-61 \\
 & \Rightarrow y=60 \\
\end{align}$
From the above solution, we got the value of x and y as 61 units and 60 units.
Now, we got the value of hypotenuse as 61 units, base, and perpendicular as 11 units and 61 units.
We know the area of a right triangle is equal to one half of the base multiplied by the height.

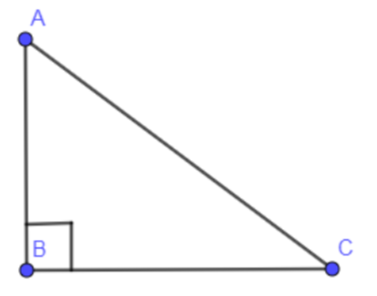
We have found in the above solution, the base is BC equal to 11 units and AB is the height is equal to 60 units.
Area of triangle ABC is equal to:
$\begin{align}
  & \dfrac{1}{2}\left( base \right)\left( height \right) \\
 & =\dfrac{1}{2}\left( 11 \right)\left( 60 \right) \\
 & =30\left( 11 \right)=330\text{sq}\text{. units} \\
\end{align}$
Hence, we got the area of triangle ABC as 330 sq. units which is more than 300.
Hence, the correct option is (d).

Note: The possible mistake that could happen in this problem is that you might have skipped one of the two cases that we have shown above when the side of length 11 is the hypotenuse and when it is not so if you miss the main case when 11 is not a hypotenuse then you won’t get an answer but if you miss the case when 11 is a hypotenuse then you are lucky and you get the right answer. But it is not necessary that your luck will always be in your favor so it is better to take both of the cases.