Question

All faces of a cube with a 4-meter edge are covered with striped paper. If the cube is then cut into cubes with 1-meter edges, how many of the 1-meter cubes have striped paper on exactly one face?
(A) 24
(B) 36
(C) 48
(D) 60
(E) 69

Answer 1

Hint: The edge length of the bigger and smaller cube are 4 meters and 1 meter respectively. Calculate the total number of smaller cubes using the formula, the number of smaller cubes = \[\dfrac{Volume\,of\,bigger\,cube}{Volume\,of\,smaller\,cube}\] . When the bigger cube of edge length 4 meters is cut into smaller cubes of edge length 1 meter then, the bigger cube will get divided into 4 layers, and each layer consists of 16 cubes. Now, draw the diagram of one face of the cube. The number of cubes that have the striped paper on exactly one face is 4 and there are six faces of a cube. Now, solve it further and calculate the total number of smaller cubes that have the striped paper on exactly one face.

Complete step by step answer:
According to the question, we are given that all faces of a cube are covered with striped paper and the cube is then cut into smaller cubes. We are asked to find the number of cubes that have a striped paper on exactly one face.
The edge length of the bigger cube = 4 m ………………………………………..(1)
The edge length of the smaller cube = 1 m ………………………………………(2)
We know the formula, the number of smaller cubes = \[\dfrac{Volume\,of\,bigger\,cube}{Volume\,of\,smaller\,cube}\] …………………………………...(3)
We also know the formula, the area of square = \[{{\left( edge \right)}^{3}}\] …………………………………………(4)
Now, from equation (1), equation (2), equation (3), and equation (4), we get
The number of smaller cubes = \[\dfrac{{{\left( 4m \right)}^{3}}}{{{\left( 1m \right)}^{3}}}=64\] ……………………………….(5)
When the bigger cube of edge length 4 meters is cut into smaller cubes of edge length 1 meter then, the bigger cube will get divided into 4 layers ………………………………….(6)
Now, from equation (5) and equation (6), we get
The number of smaller cubes in each layer = \[\dfrac{64}{4}=16\] ………………………………….(7)
Let us draw a diagram of one face of the cube.
 

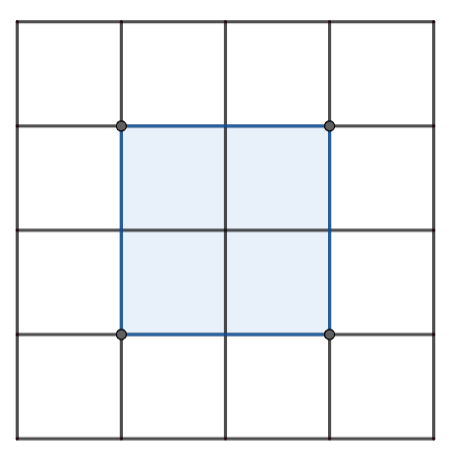
In the above diagram, we can observe one face of the cube,
The number of cubes that have the striped paper on exactly one face = 4 ……………………………………..(8)
We know the property that a cube has six faces ……………………………………(9)
Now, from equation (8) and equation (9), we get
For six faces, the number of squares that have the striped paper on exactly one face = \[6\times 4\] = 24 …………………………………..(10)
Therefore, the number of squares that have the striped paper on exactly six faces is 24.

So, the correct answer is “Option A”.

Note: For this type of question, one should remember the formula to calculate the total number of smaller cubes, the number of smaller cubes = \[\dfrac{Volume\,of\,bigger\,cube}{Volume\,of\,smaller\,cube}\] . Now, observe one face of the cube then, count the number of smaller cubes having the striped paper on exactly one face and multiply it with the total number of faces of the cube to get the total number of smaller cubes having the striped paper on exactly one face.