Question

$A\left( {x,y} \right),B\left( {{x_2},{y_2}} \right){\text{ and C}}\left( {{x_3},{y_3}} \right)$ are \[3\] non-collinear points in coordinate plane. Number of parallelograms that can be drawn with these \[3\] points as vertices are:

Answer 1

Hint:For this question they have to draw these points on a coordinate plane and then only we will be able to proceed with the question further. so we have to draw the figure in a coordinate system.So then we can say how many parallelograms present in it.


Complete step by step solution:

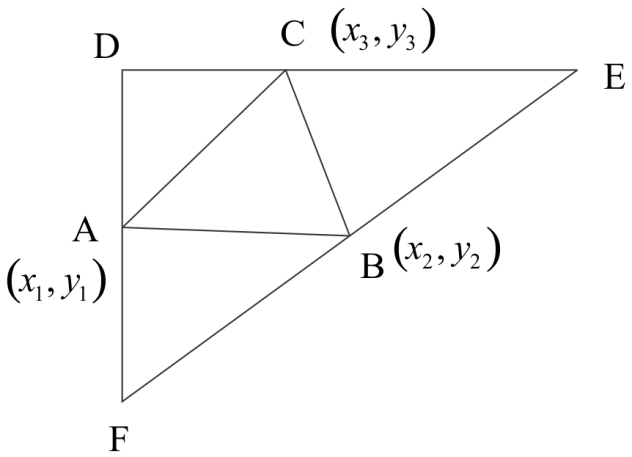
You can see the figure.
By this figure, we can say that there exists almost \[3\] parallelogram. which are \[ - ABCD,ABEC,ACBF\] .
\[{\mathbf{ABCD}},{\text{ }}{\mathbf{ABEC}}{\text{ }}{\mathbf{and}}{\text{ }}{\mathbf{ACBF}}\]. These \[{\mathbf{3}}\]parallelograms are possible.

Note: After plotting vertices on a plane joining the coordinates will give us the required parallelograms.There is no other method to solve the problem..so use this method to solve the problem..by drawing you can get a full concept of a figure.