Question

A$\left( {{x}_{1}},{{y}_{1}} \right)$ , B$\left( {{x}_{2}},{{y}_{2}} \right)$ , C $\left( {{x}_{3}},{{y}_{3}} \right)$are three vertices of a triangle ABC. $lx+my+n=0$ is an equation of the line L.
If L intersects the sides BC, CA and AB of the triangle ABC at P,Q,R, respectively, then $\dfrac{BP}{PC}\times \dfrac{CQ}{QA}\times \dfrac{AR}{RB}$ is equal to :
(a). -1
(b). $-\dfrac{1}{2}$
(c). $\dfrac{1}{2}$
(d). 1

Answer 1

Hint: given one line cuts the all sides of the triangle. So extend the sides somewhat and then draw the line which cuts all the sides. Now find the corresponding sides and their ratio. From this you can get the side length in terms of variables as you know. By substituting side lengths in the expression they asked for we get the expression with variables which we substituted before the extending.

Complete step-by-step answer:
First extend the line BC outwards so that you can draw a line to cut all the sides AB, BC,CA.

Now draw a line parallel to L from point B. Mark the point as X as a parallel line, cuts the line their way corresponding.

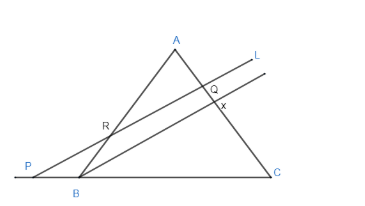
We say angle ARQ is the same as angle ABX. Angle AQR is the same as angle AXB.
So, from the above conditions from AA axiom triangles ARQ and ABX are similar.
So, we can say that their sides are proportional.
$\dfrac{AR}{QA}=\dfrac{AB}{AX}$ .
So, let $AR:AQ=x:y$ ,
So, we can say-
$AR=ax$ , $AQ=ay$ then by corresponding we get –
$BR=bx$ , $QX=by$ .
From triangles CXB and CQP we can say angles are the same.
 By corresponding angle CBX is the same as CPQ angle, and also angle CXB is same as the angle CQP.
So, from the above condition from AA axiom these both triangles are similar.
If $CX=CY$ we get $QX:CX=b:c$ .
Then, $PB:CB=b:c$ .
So, we write $BC=cz$ and $BP=bz$ .
Required expression is $\dfrac{BP}{PC}\times \dfrac{CQ}{QA}\times \dfrac{AR}{AB}$ .
By substituting all values BP, PC, CQ, QA, AR, AB.
We get expression as follows:-
$\dfrac{bz}{\left( b+c \right)z}\times \dfrac{\left( b+c \right)}{ay}\times \dfrac{ax}{bx}$ .
By cancelling common terms we get value as 1.
So, the required value of expression given is 1.
Option (D) is correct answer

Note: While taking ratios do not confuse with a, b, c and x, y, z. one of them is kept common to get cancelled and give us the ratio we need. We say that before ratio is a:b so we take “ax”, “bx” now next step we take ratio of second term and new line to be x:y so we need the other side to be “by” for b to get cancel and give required ratio of x:y from second term and new term.