Question

AD is an altitude of an equilateral triangle ABC. On AD as the base, another equilateral triangle ADE is constructed, then area (Triangle ADE): area (Triangle ABC) = 3:4.
(a) True
(b) False

Answer 1

Hint: As we have both the triangles as equilateral triangles, so they are similar. We know that if triangle ABC is congruent to triangle PQR, then, \[\dfrac{Ar\left( \Delta ABC \right)}{Ar\left( \Delta PQR \right)}={{\left( \dfrac{AB}{PQ} \right)}^{2}}={{\left( \dfrac{BC}{QR} \right)}^{2}}={{\left( \dfrac{AC}{PR} \right)}^{2}}.\] So, we compare the sides to find the ratio of the area between triangle ADE and triangle ABC.

Complete step-by-step solution:
We are given that ABC is an equilateral triangle. Let us consider its side as ‘a’. So, we get,
\[AB=BC=AC=a......\left( i \right)\]
AD is the altitude through while we will construct another triangle ADE.

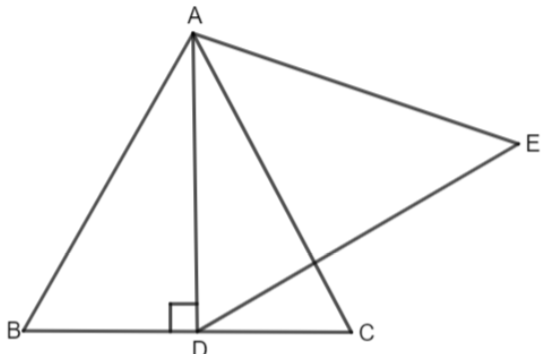
We know that in triangle ABC, altitude is the perpendicular bisector. So, we have,
\[BD=DC......\left( ii \right)\]
\[BC=BD+DC\]
From (ii), we have BD = DC, so we get,
\[\Rightarrow BC=BD+BD\]
\[\Rightarrow BC=2BD\]
So, we get,
\[\Rightarrow \dfrac{BC}{2}=BD\]
Noe from (i), we get,
\[BD=\dfrac{a}{2}....\left( iii \right)\]
As AD is a perpendicular bisector, we get triangle ABD as right triangle. Now, applying Pythagoras theorem in triangle ABD which says
\[A{{D}^{2}}+B{{D}^{2}}=A{{B}^{2}}\]
From here, we get,
\[A{{D}^{2}}=A{{B}^{2}}-B{{D}^{2}}\]
Using the value of (i) and (iii), we get,
 \[A{{D}^{2}}={{a}^{2}}-\dfrac{{{a}^{2}}}{4}\]
\[\Rightarrow A{{D}^{2}}=\dfrac{4{{a}^{2}}-{{a}^{2}}}{4}\]
\[\Rightarrow A{{D}^{2}}=\dfrac{3{{a}^{2}}}{4}\]
Now, canceling square on both the sides, we get,
\[AD=\dfrac{\sqrt{3}a}{2}.....\left( iv \right)\]
So, we get the length of the sides of the triangle ADC as \[AD=\dfrac{\sqrt{3}a}{2}.\]
As triangle ABC and triangle ADE are both equilateral triangles, this means that both the triangles have all the angles as \[{{60}^{\circ }}.\] Therefore, by AAA similarity criteria, they are similar.
So,
\[\dfrac{Ar\left( \Delta ADE \right)}{Ar\left( \Delta ABC \right)}={{\left( \dfrac{AD}{AB} \right)}^{2}}\]
Using (i) and (iv), we get,
\[\Rightarrow \dfrac{Ar\left( \Delta ADE \right)}{Ar\left( \Delta ABC \right)}=\dfrac{{{\left( \dfrac{\sqrt{3}{a}}{2} \right)}^{2}}}{{{a}^{2}}}\]
\[\Rightarrow \dfrac{Ar\left( \Delta ADE \right)}{Ar\left( \Delta ABC \right)}=\dfrac{\dfrac{3{{a}^{2}}}{4}}{{{a}^{2}}}\]
\[\Rightarrow \dfrac{Ar\left( \Delta ADE \right)}{Ar\left( \Delta ABC \right)}=\dfrac{3{{a}^{2}}}{4{{a}^{2}}}\]
\[\Rightarrow \dfrac{Ar\left( \Delta ADE \right)}{Ar\left( \Delta ABC \right)}=\dfrac{3}{4}\]
So, we get,
\[\dfrac{Ar\left( \Delta ADE \right)}{Ar\left( \Delta ABC \right)}=\dfrac{3}{4}\]
Hence, option (a) is the right answer.

Note: The alternate method to find AD, i.e the altitude is as follows. We know that the area of the equilateral triangle is also given as
\[\text{Area}=\dfrac{\sqrt{3}}{4}\times {{\left( \text{side} \right)}^{2}}\]
In triangle ABC with base BC and altitude AD, we get,
\[\text{Area of }\Delta \text{ABC}=\dfrac{1}{2}\times BC\times AD\]
Also,
\[\text{Area of }\Delta ABC=\dfrac{\sqrt{3}}{4}{{\left( \text{side} \right)}^{2}}\]
\[\Rightarrow \text{Area of }\Delta ABC=\dfrac{\sqrt{3}}{4}\times B{{C}^{2}}\]
So comparing both, we get,
\[\dfrac{1}{2}\times BC\times AD=\dfrac{\sqrt{3}}{4}\times B{{C}^{2}}\]
Solving for AD, we get,
\[\Rightarrow AD=\dfrac{\sqrt{3}}{4}\times B{{C}^{2}}\times \dfrac{2}{BC}\]
\[\Rightarrow AD=\dfrac{\sqrt{3}}{2}\times BC\]
As BC = a, we can write as,
\[\Rightarrow AD=\dfrac{\sqrt{3}}{2}a\]