Question

Acceleration is a ________ quantity
a) vector
b) scalar
c) tensor
d) None of the above

Answer 1

Hint: A scalar is a number or a constant which just has a magnitude but no specified direction. A vector is a scalar only but it has a direction associated with it. Speaking about a tensor quantity it has both magnitude as well as direction like a vector but it has different magnitude for different direction or orientation. Hence using above conditions we can categorize acceleration accordingly.

Complete step by step answer:

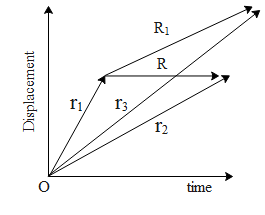
If we consider the above diagram, let us say a particle moves from ${{r}_{1}}\text{ to }{{r}_{2}}$ in time t. Hence the displacement of the particle is given by R. Let us assume the particle is experiencing constant force. Hence by Newton’s second law acceleration of the particle is $\overline{a}=\dfrac{F}{m}$ where F is the force on the particle and m is the mass of the particle. From the above diagram the velocity of the particle is given by $\dfrac{dR}{dt}\widehat{R}$ and its acceleration is given by $\dfrac{{{d}^{2}}R}{{{(dt)}^{2}}}\widehat{R}.....(1)$ where $\widehat{R}$ is a unit vector. Now let us say the particle moves from position ${{r}_{1}}\text{ to }{{r}_{3}}$ at the same time t. Hence its displacement is given by ${{R}_{1}}$, its velocity is given by $\dfrac{d{{R}_{1}}}{dt}\widehat{{{R}_{1}}}$ and acceleration is given by $\dfrac{{{d}^{2}}{{R}_{1}}}{{{(dt)}^{2}}}\widehat{{{R}_{1}}}.....(2)$ where $\widehat{{{R}_{1}}}$ is the unit vector along the displacement.
It is to be noted that $\dfrac{{{d}^{2}}R}{{{(dt)}^{2}}}=\dfrac{{{d}^{2}}{{R}_{1}}}{{{(dt)}^{2}}}$ are the same since acceleration is constant given by $\overline{a}=\dfrac{F}{m}$, it is just that they are directed in different direction. This conclusion drawn is in accordance with the vector definition given in the hint.

Hence the correct answer to the question is option a.

Note:
It is to be noted that with change in direction the acceleration of the particle can change. But this is only possible if the force on the particle changes. Hence one may conclude that the quantity is tensor, but that’s not true since a tensor quantity changes when there is change in orientation itself without the change in any other factors.