Question

How is acceleration found from a velocity-time graph?

Answer 1

Hint:A velocity time graph is one which tells us velocity of an object at every instant in time. It not only tells us the magnitude of velocity but also tells us in which direction the object is moving. Acceleration of the body is defined as the change in velocity per unit time. If we say that the acceleration of a body is $5m{{s}^{-2}}$, then it actually means that the body is gaining a velocity of $5m{{s}^{-1}}$ at every second of time.

Complete answer:
If the graph stays above the axis depicting time, then we can decipher that the velocity is positive and the object is moving in one particular direction but if the graph falls below the axis depicting time, then we say that the object is moving in the completely opposite direction and the velocity is negative.
To find the acceleration, divide the velocity change over an interval of time with that particular interval of time itself.
Acceleration, $a=\dfrac{\Delta v}{\Delta t}$

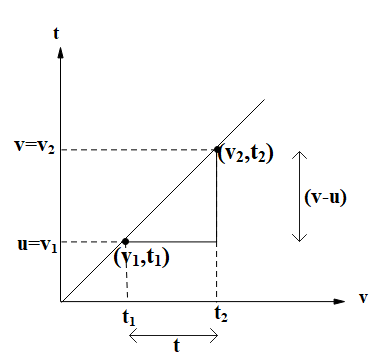
$\Rightarrow a=\dfrac{{{v}_{2}}-{{v}_{1}}}{{{t}_{2}}-{{t}_{1}}}$
$\Rightarrow a=\dfrac{v-u}{t}$
Here,
$v=$final velocity
$u=$initial velocity
$t=$time duration in which the velocity change is being observed.
When the graph is a straight line, the acceleration remains constant, that is, the body is undergoing a uniformly accelerated motion. When the graph is parallel to the axis depicting time, then the velocity of the body is a constant and hence, the acceleration of the body is zero.

Note:
The higher the acceleration, the steeper would be the graph, that is, it tends to be nearer to the axis depicting velocity. Also, the higher the acceleration, the bigger will be the slope of the graph. The velocity time graph does not give any information about the position of the object.