Question

ABCDEF is a regular hexagon with a center at the origin such that \[AD + EB + FC = \lambda ED\]. Then \[\lambda \] is equal to?
A.\[2\]
B.\[4\]
C.\[6\]
D.3

Answer 1

Hint: In order to find the value of $\lambda $ for the given equation, we need to know about the details of the hexagon. Hexagon is a two-dimensional geometrical shape that is made of six sides, having the same or different dimensions of length. A hexagon is either regular (with \[6\] equal side lengths and angles) or irregular (with \[6\] unequal side lengths and angles).

Complete answer:
Since, we know that Hexagons can be classified based on their side lengths and internal angles. But we are given a regular hexagon. And, we know that
Regular Hexagon: A regular hexagon is one that has equal sides and angles. All the internal angles of a regular hexagon are \[{120^ \circ }\]. The exterior angles measure \[{60^ \circ }\]. The sum of the interior angles of a regular hexagon is \[{720^ \circ }\].

And, we are given with a regular hexagon ABCDE, so according to this the represented figure is:

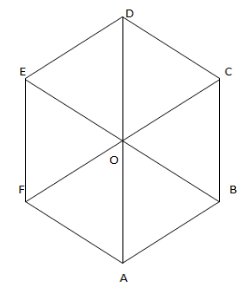
In this figure all the sides are equal and also, we know that each triangle formed by the diagonals will be an equilateral triangle, that means:

So, In triangle EOD:
$ED = EO = OD$

Similarly, for all remaining triangles, the condition is the same.

Since, the length of the sides is equal and also each side of the triangle formed are equal that means there will be twelve equal sides followed as:
$AB = BC = CD = DE = EF = FA = EO = OD = OC = OB = OA = OF$ ……(1)

Now, For AD, we can write it as:
$AD = AO + OD$
And, since we know that $ED = AO = OD$, so we can write:
$ \Rightarrow AD = OD + OD = 2OD$ ……(2)

Similarly, we can write for other sides as:
For EB, we can write it as:
$EB = EO + OB$
And, since we know that $ED = EO = OB$ , so we can write:
$ \Rightarrow EB = EO + EO = 2EO$ ……(3)

For FC, we can write it as:
$FC = FO + OC$
And, since from 1 we can see that $ED = FO = OC$, so we can write:
$ \Rightarrow FC = ED + ED = 2ED$ ……(4)

Adding 2, 3 and 4, we get:

\[
  AD + EB + FC \\
   \Rightarrow 2OD + 2EO + 2ED \\
 \]

Taking 2 common from EO and OD, we get:

\[ \Rightarrow 2\left( {OD + EO} \right) + 2ED\]
\[ \Rightarrow 2\left( {EO + OD} \right) + 2ED\]

Since, \[EO + OD = ED\], so we get:
\[
   \Rightarrow 2ED + 2ED \\
   = 4ED \\
 \]

Hence, we get:
\[AD + EB + FC = 4ED\]
On comparing \[AD + EB + FC = 4ED\]with \[AD + EB + FC = \lambda ED\] we get:
\[\lambda = 4\]
Therefore option (2) is the correct answer.

Note:
There are other various types of hexagon we have such as Irregular hexagon- which means all the sides are of different length and also internal angles are not equal. But, the sum of interior angles would not change.
Some other angles would be Convex hexagon, concave hexagon etc.