Question

ABCDE is a regular Pentagon. The bisector of angle A of the Pentagon meets the side CD in M. Then the measure angle AMC is
\[\begin{align}
  & A{{.54}^{\circ }} \\
 & B{{.45}^{\circ }} \\
 & C{{.90}^{\circ }} \\
 & D{{.100}^{\circ }} \\
\end{align}\]

Answer 1

Hint: We will use formula for finding interior angles of a regular Pentagon which is given by each interior angle of regular polygon $\Rightarrow \dfrac{2n-4}{n}\times {{90}^{\circ }}$ where n is number of side of a polygon. As we are given that, angle A is bisected by AM. Hence, a quadrilateral ABCM is obtained where we now know three of the angles and use them in the angle sum property of quadrilateral to find the fourth angle. Angle sum property of quadrilateral tells us that, sum of angles of a quadrilateral is equal to ${{360}^{\circ }}$

Complete step-by-step answer:
Here, we are given a regular Pentagon which is a polygon with 5 sides. As we know, each interior angle of regular polygon is given by $\Rightarrow \dfrac{2n-4}{n}\times {{90}^{\circ }}$ where n is the number of sides of polygon. As we have to find interior angle of regular Pentagon, therefore, we will put n = 5 in formula to get,
Each interior angle of Pentagon is given by:
\[\Rightarrow \dfrac{2\left( 5 \right)-4}{5}\times {{90}^{\circ }}=6\times {{18}^{\circ }}={{108}^{\circ }}\]

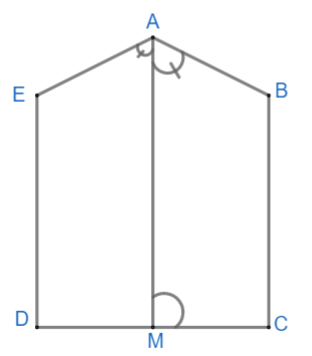
From diagram we can say that, $\angle A=\angle B=\angle C=\angle D=\angle E={{180}^{\circ }}$ since AM bisects angle A therefore, AM divides angle A into equal angles $\angle EAM\text{ and }\angle MAB$
Therefore,
\[\begin{align}
  & \angle MAB=\dfrac{1}{2}\angle A \\
 & \Rightarrow \angle MAB=\dfrac{1}{2}\left( {{108}^{\circ }} \right)={{54}^{\circ }} \\
\end{align}\]
From the diagram, we can clearly see that ABCM forms a quadrilateral. As we know, the sum of angles of a quadrilateral is equal to ${{360}^{\circ }}$. Hence, \[\Rightarrow \angle MAB+\angle B+\angle C+\angle AMC={{360}^{\circ }}\]
We have calculated the value of $\angle MAB,\angle B\text{ and }\angle C$ already. Putting them in above equation, we get:
\[\begin{align}
  & {{54}^{\circ }}+{{108}^{\circ }}+{{108}^{\circ }}+\angle AMC={{360}^{\circ }} \\
 & \Rightarrow {{270}^{\circ }}+\angle AMC={{360}^{\circ }} \\
 & \Rightarrow \angle AMC={{90}^{\circ }} \\
\end{align}\]
So, the correct answer is “Option C”.

Note: In this type of question we should firstly see which type of pentagon is given in the question, a polygon is regular when all angles are equal and all sides are equal otherwise it is "irregular". Students should take care while calculating interior angles in the Pentagon. We should draw diagrams for better understanding of these types of sums.