Question

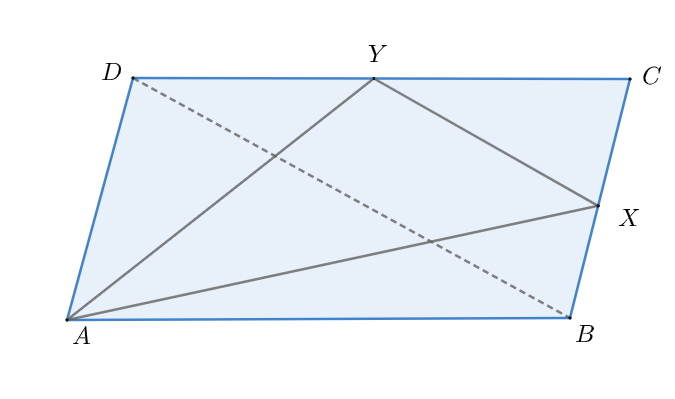
$ABCD$ is parallelogram $X$ and $Y$ are the midpoints of $BC$ and $CD$ respectively. Then \[\text{ar}\left( \text{parallelogram }ABCD \right)\] is

Answer 1

Hint: Problems of this type can be easily solved using the properties of triangles i.e., a median of a triangle divides the triangle into two parts. We assume the area of the given parallelogram to be a value $x$ and upon doing that we find the relationship between the area of the parallelogram and the triangles inside the parallelogram using the above property. Thus, we will reach to the desired result of the given problem.

Complete step-by-step answer:
Let us assume the area of the parallelogram $ABCD$ is $x$ .
From the properties of geometrical shapes and surfaces we know that the diagonals of a parallelogram divide that parallelogram in two parts having same area.
Hence, we can say $\Delta DBC=\dfrac{1}{2}x$ .
It is already given in the question that $X$ and $Y$ are the midpoints of $BC$ and $CD$ respectively.
Now, we draw a line joining the two points D and X as shown below

As, DX is also a median of $\Delta DBC$ the median divide it into two as
$\Delta CXD=\dfrac{1}{2}\Delta DBC=\dfrac{1}{4}x$
Also, the line XY which is a median dividing the triangle $\Delta CXD$ into two as
$\Delta CXY=\dfrac{1}{2}\Delta CXD=\dfrac{1}{8}x$
On the other hand, AX being a median of $\Delta ABC$ divides it into two as
$\Delta ABX=\dfrac{1}{2}\Delta ABC=\dfrac{1}{4}x$
Similarly, AY being the median of $\Delta ACD$ divides it into two as
$\Delta AYD=\dfrac{1}{2}\Delta ACD=\dfrac{1}{4}x$
From, the above figure we can write that
$\Rightarrow \Delta AXY=area(ABCD)-\left\{ \Delta CXY+\Delta ABX+\Delta AYD \right\}$
Substituting the values in the above equation we get
$\Rightarrow \Delta AXY=x-\left\{ \dfrac{1}{8}x+\dfrac{1}{8}x+\dfrac{1}{4}x \right\}$
$\Rightarrow \Delta AXY=x-\left\{ \dfrac{1}{8}x+\dfrac{1}{4}x+\dfrac{1}{4}x \right\}$
$\Rightarrow \Delta AXY=\dfrac{3}{8}x$
$\Rightarrow x=\dfrac{8}{3}\Delta AXY$
Therefore, \[\text{ar}\left( \text{parallelogram }ABCD \right)\] is $\dfrac{8}{3}\Delta AXY$ .

Note: Students must be very careful while dealing with such problems so that silly mistakes in this type of complicated calculations can be avoided. Also, students must keep in mind that the properties of triangles are applied properly and accordingly to get the correct solution of this problem.