Question

ABCD is parallelogram and APQ is a straight-line meeting BC at P and DC produced at Q. Prove that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.

Answer 1

Hint: First, we will draw a figure as per data given in question. So, we will have figure as

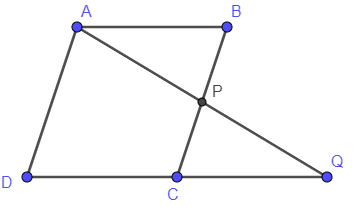
Then for triangle $\Delta ABP$ and $\Delta QCP$ we will prove that All the angles of triangle $\Delta ABP$ and $\Delta QCP$ are equal. Then, we will assume the length of sides of the parallelogram \[AB=CD=a\] and \[BC=AD=b\] . Then we will take ratio of two sides of $\Delta ABP$ and $\Delta QCP$ equal to $\alpha $ i.e. \[\dfrac{PC}{PB}=\dfrac{QC}{AB}=\dfrac{\alpha }{1}\] . Then, at last we will find the area of ABCD \[=AB\times BC\] and the rectangle formed by BP and DQ \[=BP\times DQ\] . We will get both areas equal.

Complete step by step answer:
Here, we will first draw the figure as per data given in question. So, we will get figure as
   

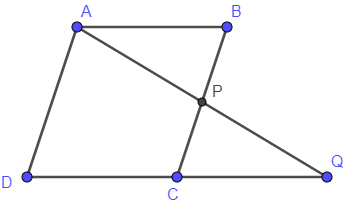
We will consider $\Delta ABP$ and $\Delta QCP$ . We can see that angle $\angle BAP$ and $\angle CQP$ are alternate angles. Alternate angles are formed when a line crosses two other lines, that lie on opposite sides of the transversal line and on opposite relative sides of the other lines. If two lines crossed are parallel, the alternate angles are equal.
So, here AB and CD are parallel lines and transversal is BC.
Thus, we can say that \[\angle BAP=\angle CQP\] ………………………….(1)
Similarly, with the same concept of alternate angles we can say that
\[\angle ABP=\angle QCP\] …………………..(2)
Now, using the concept of vertically opposite angles i.e. the angles opposite each other when two lines cross. They are always equal. So, in figure we can see that line AQ and BC cross each other at point P. So, we can write it as
\[\angle APB=\angle QPC\] ………………………………(3)
From this, we get figure as
  

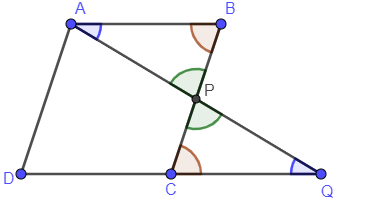
Thus, \[\Delta ABP\sim \Delta QCP\] .
So, we can take ratio of length of two sides of $\Delta ABP$ and $\Delta QCP$ is equal to let say \[\alpha \] so, we can write it as
\[\dfrac{PC}{PB}=\dfrac{QC}{AB}=\dfrac{\alpha }{1}\]
So, from this we can write PB as \[\dfrac{PC}{PB}=\dfrac{\alpha }{1}\Rightarrow PB=\dfrac{PC}{\alpha }\] ………………………(4)
In the same way, we get \[\dfrac{QC}{AB}=\dfrac{\alpha }{1}\Rightarrow QC=AB\cdot \alpha \] ………………………(5)
Now, let us say that the length of side \[AB=CD=a\] and \[BC=AD=b\] .
So, we can write BC as \[BC=PB+PC\]. On substituting the values in this equation, we get as
\[b=PB+PB\cdot \alpha \] ……………………………..(6)
From equation (4), we get the value of PC as \[PC=PB\cdot \alpha \] .
So, from equation (6), we get value of PB as
\[b=PB\left( 1+\alpha \right)\]
\[\dfrac{b}{\left( 1+\alpha \right)}=PB\] ………………………………(7)
From the figure, we can QD as \[QD=QC+CD\] . On substituting the values from equation (5) and we have assumed AB, CD as ‘a’, we get QD as
\[QD=AB\cdot \alpha +a\]
\[QD=a\cdot \alpha +a=a\left( \alpha +1 \right)\] …………………………….(8)
Now, we have to prove the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.
So, we will find area of parallelogram ABCD \[=AB\times BC\]
On substituting the values, we get area as
Area of ABCD \[=a\times b\] ……………………….(9)
Again, we will find area of rectangle formed by BP and DQ which can we given as
\[=BP\times DQ\]
On substituting the values from equation (7) and (8), we get as
\[=\dfrac{b}{\left( 1+\alpha \right)}\times a\left( \alpha +1 \right)\]
On cancelling the terms, we get as
\[=b\times a\] …………………….(10)
Thus, values of equation (9) and (10) are equal, so we can say that the rectangle obtained by BP and DQ is equal to the rectangle contained by AB and BC.
Hence, proved.

Note: Students should know all the concepts of alternate angles and vertically opposite angles. Another method to prove this is by taking the ratio of corresponding sides i.e. \[\dfrac{PC}{PB}=\dfrac{QC}{AB}\] . On solving this and adding $AB\times PB$ on both sides, we will get as
$AB\times PB+QC\times PB=AB\times PC+AB\times PB$
On solving this by taking PB common from both sides, we will get as
$PB\left( AB+QC \right)=AB\left( PC+PB \right)$ Which we can write it as from figure as
$PB\left( DC+QC \right)=AB\times BC$
Thus, we will get as $PB\times DQ=AB\times BC$ . Hence, proved.