Question

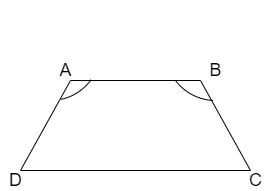
ABCD is a trapezium in which \[AB\parallel CD\] and \[AD=BC\] then prove that \[\angle A=\angle B\]

Answer 1

Hint: We solve this problem by using a certain construction such that there will be a parallelogram drawn by extending AB and drawing a line C to extended AB
Then we use the properties of parallelogram and triangle to prove the required result.
(1) We have the condition of a parallelogram that is the opposite angles and opposite sides are equal.
(2) We have the condition of a triangle that is the angles opposite to equal sides are equal.

Complete step by step answer:
We are given that ABCD is a trapezium in which \[AB\parallel CD\] and \[AD=BC\]
Now, let us extend side AB and draw a line from C to extended AB to form a parallelogram as follows

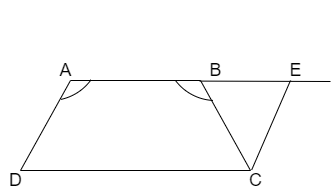
Here, we can see that AECD is a parallelogram.
We know that the condition of a parallelogram that is opposite two sides are equal.
By using the above condition we get
\[\Rightarrow AD=EC\]
But we are given that \[AD=BC\] so that we can write the above equation as
\[\Rightarrow EC=BC\]
We know that the condition of triangle that is the angles opposite to equal sides are equal.
By using the above condition to triangle \[\Delta BCE\] then we get
\[\Rightarrow \angle CBE=\angle CEB\]
Here, we can see that the vertex B have two angles such that sum of all angles will be equal to \[{{180}^{\circ }}\]
By using the above condition to angles at vertex B then we get
\[\Rightarrow \angle ABC+\angle CBE={{180}^{\circ .}}\]
By substituting the result \[\angle CBE=\angle CEB\] in above equation then we get
\[\begin{align}
  & \Rightarrow \angle ABC+\angle CEB={{180}^{\circ }} \\
 & \Rightarrow \angle ABC={{180}^{\circ }}-\angle CEB.........equation(i) \\
\end{align}\]
We know that the opposite sides of parallelogram are parallel that is \[AD\parallel CE\]
Here, we can see that AE is transversal to parallel lines AD and CE
We know that interior angles of two parallel lines add up to \[{{180}^{\circ }}\]
By using the above condition to parallel lines AD and CE taking AE as transversal then we get
\[\begin{align}
  & \Rightarrow \angle DAB+\angle CEB={{180}^{\circ }} \\
 & \Rightarrow \angle DAB={{180}^{\circ }}-\angle CEB..........equation(ii) \\
\end{align}\]
By comparing the equation (i) and equation (ii) then we get
\[\begin{align}
  & \Rightarrow \angle DAB=\angle ABC \\
 & \Rightarrow \angle A=\angle B \\
\end{align}\]
Hence the required result has been proved.

Note:
 We need to note that the condition the angles opposite to equal sides are equal is applicable only for triangles not for all figures.
Let us assume that the above condition is applicable for given trapezium ABCD
Here, we are given that \[AD=BC\]
Here, we can see that the side AD has two opposite angles as \[\angle B,\angle C\]
Here, both angles are opposite to side AD so that we cannot use the condition.
Similarly, side BC has two opposite angles \[\angle A,\angle D\]
Here, we cannot take any set of two angles that changes the property of ABCD.