Question

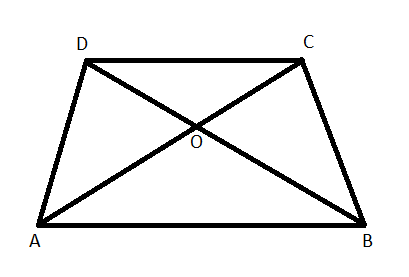
ABCD is a trapezium in which AB || CD and AB = 2CD. If its diagonals intersect at each other at O, then the ratio of the area of triangle ABC and triangle COD is:
a. 1:2
b. 2:1
c.1:4
d.4:1

Answer 1

Hint: As given in the question that AB is parallel to CD, we take two triangles namely triangle AOB and triangle COD. Now, we have to prove that the triangles are similar. As in triangle AOB and triangle COD, \[\angle OAB=\angle OCD\] by alternate interior angles, $\angle OBA=\angle ODC$ by alternate interior angles and $\angle AOB=\angle DOC$ by vertically opposite angles. By above three facts triangle ABC is similar to triangle COD using AAA(Angle-Angle-Angle) property. From the result obtained, we can easily say that the ratio of AB and CD is equal to the ratio of AO and CO and the ratio of OB and OD are equal. Now, we can easily find the ratio of 2CD and CD and by squaring the ratio we get the ratio of area of both triangles.

Complete step-by-step answer:
As given in the question that they AB is parallel to CD. Now we take triangle AOB and triangle COD to prove that both the triangles are similar.
So, we have to prove both the triangles $\Delta AOB\text{ and }\Delta COD$ are similar.
Proof: AB||CD (given)
In $\Delta AOB\text{ and }\Delta COD$
$\angle OAB=\angle OCD$ (Using alternate interior angles)
$\angle OBA=\angle ODC$ (Using alternate interior angles)
$\angle AOB=\angle DOC$ (Using vertically opposite angles)
$\Delta AOB\tilde{\ }\Delta COD$ (Using AAA similarly)
$\therefore $ The triangles AOB and COD are similar.
Hence, proved.
We know that,
$\begin{align}
  & \dfrac{Area\text{ of }\Delta \text{AOB}}{Area\text{ of }\Delta \text{COD}}={{\left( \dfrac{AB}{CD} \right)}^{2}}={{\left( \dfrac{AO}{CO} \right)}^{2}}={{\left( \dfrac{OB}{OD} \right)}^{2}} \\
 & {{\left( \dfrac{2CD}{CD} \right)}^{2}}=\dfrac{4}{1}=4:1 \\
\end{align}$
$\therefore $ The ratio of area of triangle AOB and COD is $4:1$.
Hence, option (d) is correct.
Note: The key steps for solving this problem is the proof of similarity of both the triangles. Once both the triangles are similar then by using the ratio of sides, we can easily evaluate the ratio of area of mentioned triangles. So, the knowledge of similar figures is required to solve this problem.