Question

ABCD is a square with side a, with centers A, B, C and D four circles are drawn such that each circle touches externally two of the remaining three circles. Let S be the area of the region in the interior of the square and exterior of the circle. Then, maximum value of S is
\[\begin{align}
  & A.{{a}^{2}}\left( 1-\pi \right) \\
 & B.{{a}^{2}}\left( \dfrac{4-\pi }{4} \right) \\
 & C.{{a}^{2}}\left( \pi -1 \right) \\
 & D.\dfrac{\pi {{a}^{2}}}{4} \\
\end{align}\]

Answer 1

Hint: For this sum, we will first draw a diagram for better understanding of the question. Since we have to find maximum area of region in interior of square and exterior of circle, we can find area of square and area of portion of circle inside square and then subtract them to find maximum region. We use formula of finding area of square and area of circle which are as follows:
(i) Area of square $\Rightarrow {{a}^{2}}$ where ‘a’ is the side of the square.
(ii) Area of circle $\Rightarrow \pi {{r}^{2}}$ where ‘r’ is radius of circle.

Complete step-by-step answer:
Let us first draw a diagram in which ABCD is a square and four circles are drawn with A, B, C, D as centers having the same radius.

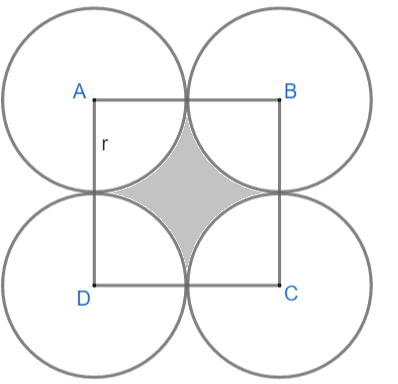
We are given a side of the square as 'a'. Therefore, area of square is $\Rightarrow {{a}^{2}}$
\[\text{Area of square}={{a}^{2}}\cdots \cdots \cdots \cdots \left( 1 \right)\]
Since, A, B, C, D are centers and circles touch each other, therefore, the radius of the circle will be equal to half of the side of the square. Therefore, radius of circle $\Rightarrow \dfrac{a}{2}$
As we can see, ${{\dfrac{1}{4}}^{th}}$ portion of each circle is inside the square and we require only the region inside the square, hence, area of one circle inside square will be $\dfrac{1}{4}\pi \times {{\left( \dfrac{a}{2} \right)}^{2}}$
Area of 4 circles inside the square \[\Rightarrow 4\times \dfrac{1}{4}\times \pi \times {{\left( \dfrac{a}{2} \right)}^{2}}=\dfrac{\pi {{a}^{2}}}{4}\cdots \cdots \cdots \cdots \left( 2 \right)\]
To find maximum value of S, the region in the interior of square and exterior of circles, we will need to find difference of area of square and area of portion of circles inside the square. Thus,
S = area of square - area of portion of circles inside the square.
From (1) and (2) we find that:
\[\begin{align}
  & S={{a}^{2}}-\dfrac{\pi {{a}^{2}}}{4} \\
 & \Rightarrow S=\left( \dfrac{4-\pi }{4} \right){{a}^{2}} \\
\end{align}\]
Hence, option B is the correct answer.

So, the correct answer is “Option B”.

Note: Students should always draw diagrams for these types of questions. They should be careful while calculating the radius of the circle. Since the shaded region is not particularly any shape whose area we can find directly, so, we had to find the area of the square and area of the circle and then subtract them. Students can make the mistake of subtracting the area of all four circles fully from square which should be taken care of.