Question

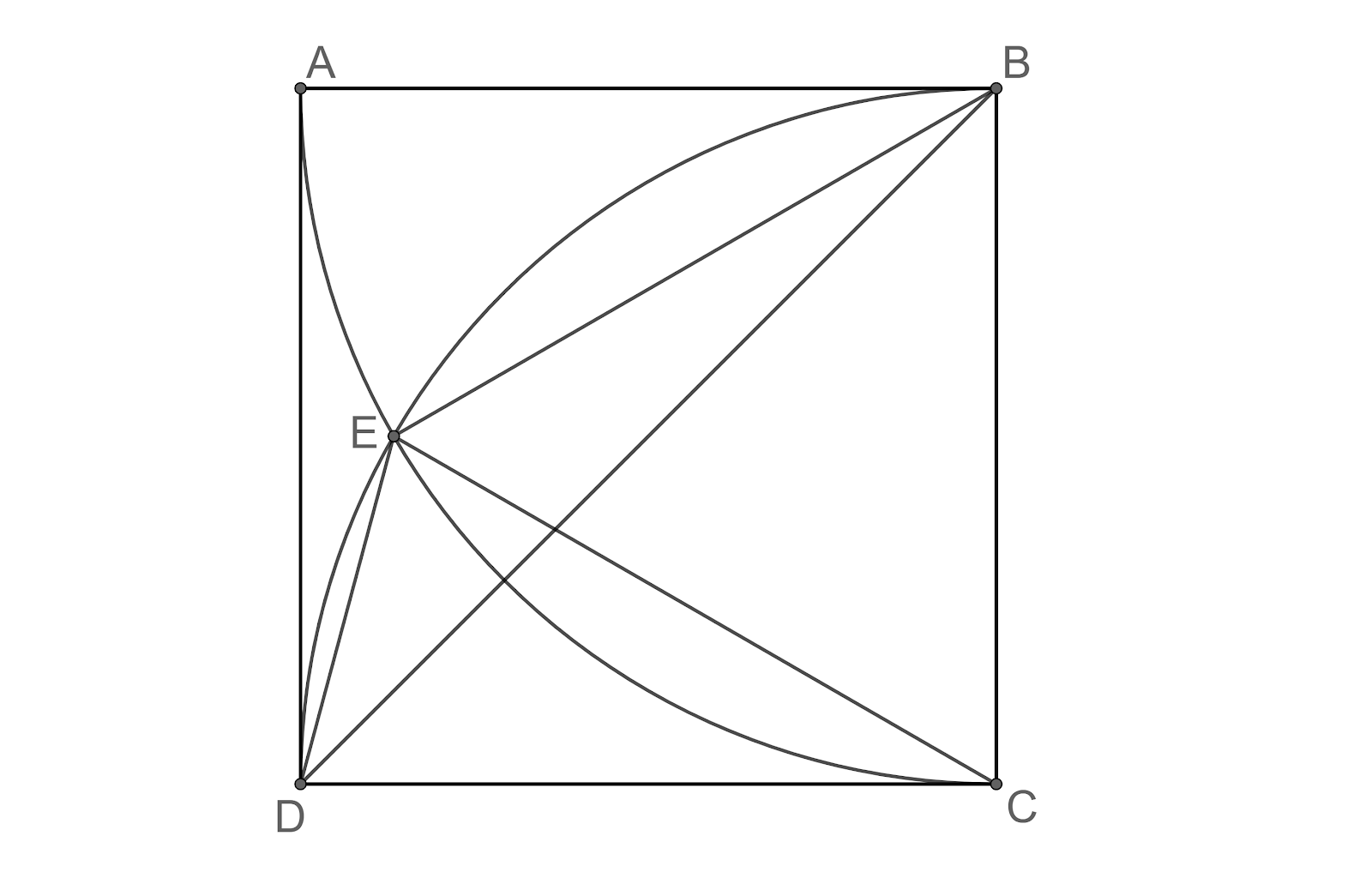
ABCD is a square. With centres B and C and radius equal to the side of the square, circles are drawn to cut one another at E inside the square. What is the value of the angle $\angle EDB$?

(a) $22{{\dfrac{1}{2}}^{\circ }}$,
(b) ${{30}^{\circ }}$,
(c) ${{15}^{\circ }}$,
(d) ${{37}^{\circ }}$.

Answer 1

Hint: We start solving the problem by finding the angles present in the triangle $\Delta BCE$ using the fact that the angles in an equilateral triangle are equal. We then use the fact that every angle at vertex in a square is ${{90}^{\circ }}$ at the vertex C to find the angle $\angle ECD$. We then find the angles in the triangle $\Delta EDC$ using the fact that the angles opposite to the equal sides are also equal. We then use the fact that diagonal bisects the angle at vertex in a square and make the necessary calculations to get the required value of answer.

Complete step-by-step answer:
According to the problem, we have given a square ABCD. We have drawn circles with centres B and C and radius equal to the side of the square. If these circles intersect at the point E, then we need to find the value of the angle $\angle EDB$.
Let us assume the length of the side of the square is ‘x’.
From the figure, we can see that the line segment CE is the radius of the circle passing through the vertices B and D. Also, the line segment BE is the radius of the circle passing through the vertices A and C. We know that the radii of these circles are equal to the length of the side of the square.
So, we get $BC=CE=BE=x$. This makes the triangle $\Delta BCE$ equilateral. We know that the angles in an equilateral triangle are equal.
So, we get $\angle BEC=\angle ECB=\angle CBE={{60}^{\circ }}$ ---(1).
We know that every angle at vertex in a square is ${{90}^{\circ }}$.
So, we get $\angle ECD+\angle ECB={{90}^{\circ }}$.
From equation (1), we get $\angle ECD+{{60}^{\circ }}={{90}^{\circ }}$.
$\Rightarrow \angle ECD={{30}^{\circ }}$ ---(2).
From the triangle $\Delta EDC$, we can see that the lengths of EC and CD are equal, which makes the triangle isosceles.
We know that the angles opposite to the equal sides are also equal.
So, we get $\angle DEC=\angle CDE$ ---(3).
We know that the sum of all angles in a triangle $\Delta EDC$ is ${{180}^{\circ }}$.
So, we get $\angle DEC+\angle CDE+\angle ECD={{180}^{\circ }}$.
From equation (2) and (3), we get $\angle CDE+\angle CDE+{{30}^{\circ }}={{180}^{\circ }}$.
$\Rightarrow \angle CDE+\angle CDE+{{30}^{\circ }}={{180}^{\circ }}$.
$\Rightarrow 2\angle CDE={{150}^{\circ }}$.
$\Rightarrow \angle CDE=\dfrac{{{150}^{\circ }}}{2}$.
$\Rightarrow \angle CDE={{75}^{\circ }}$.
We know that the diagonal bisects the angles at the vertices in square. So, we get $\angle CDB={{45}^{\circ }}$.
From the diagram, we can see that $\angle CDE=\angle CDB+\angle BDE$.
$\Rightarrow {{75}^{\circ }}={{45}^{\circ }}+\angle BDE$.
$\Rightarrow {{30}^{\circ }}=\angle BDE$.
So, we have found the value of the angle $\angle BDE$ as ${{30}^{\circ }}$.

So, the correct answer is “Option (b)”.

Note: Since E is the intersection point of both the circles and the vertices B, C are the centres of these circles, we got the lengths equal for BE and CE. We should know that diagonal bisects the angles at the vertices in the square and divides the area of the square into two equal halves. Similarly, we can also expect the problems to find the area and perimeter of the triangle $\Delta BDE$.