Question

ABCD is a square. PQRS is a square formed by joining the mid-points of AB BC CD and AD respectively. EFGH is a square formed by joining the mid-points of PQ QR RS and PS respectively. Find the sum of the perimeters of ABCD, PQRS and EFGH, if the area of the square EFGH is \[25c{{m}^{2}}\].

Answer 1

Hint: In the given question, we are given a square ABCD. We will first assume that the length of the square ABCD is ‘a’ cm. Since, the next square is formed by joining the mid points of the square ABCD, so we will use the Pythagoras formula and find the value of the side made inside the square ABCD, which is, PQRS square. And we proceed the same for the square EFGH which is made inside PQRS. Using the side of the square EFGH, we will equate its area with the given value of the area, which is, \[25c{{m}^{2}}\]. So, we will get the value of ‘a’. We will then calculate the perimeter of each of the three squares and add it up. Hence, we will have the required value asked in the question.

Complete step by step answer:
According to the given question, we are given a square ABCD.
Let us assume that the value of the side of the square ABCD be ‘a’ cm, that is, \[AB=BC=CD=AD=a\] cm.
Then, we are given that another square PQRS is formed by joining the mid-points of the square ABCD. And so, we have to find the value of the side of the square PQRS.
In \[\vartriangle APS\], using the Pythagoras theorem here, we get,
\[P{{S}^{2}}=A{{P}^{2}}+A{{S}^{2}}\]
Here, \[AP=AS=\dfrac{a}{2}cm\]
Substituting the values in the above equation, we will get,
\[\Rightarrow P{{S}^{2}}={{\left( \dfrac{a}{2} \right)}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}\]
\[\Rightarrow P{{S}^{2}}={{\dfrac{a}{4}}^{2}}+{{\dfrac{a}{4}}^{2}}\]
Calculating the expression further, we get,
\[\Rightarrow P{{S}^{2}}={{\dfrac{2a}{4}}^{2}}\]
\[\Rightarrow P{{S}^{2}}={{\dfrac{a}{2}}^{2}}\]
The value of the side PS will be,
\[\Rightarrow PS=\sqrt{{{\dfrac{a}{2}}^{2}}}\]
\[\Rightarrow PS=\dfrac{a}{\sqrt{2}}\]cm
Next, we are given that a square EFGH is formed by joining the mid-points of the square PQRS. We will have to find the value of side of the square EFGH. And we will be using the Pythagoras formula for the same.
In \[\vartriangle PHE\],
\[H{{E}^{2}}=P{{H}^{2}}+P{{E}^{2}}\]
Here, \[PH=PE=\dfrac{PS}{2}=\dfrac{a}{2\sqrt{2}}\]cm
Substituting the value of the obtained in the above Pythagoras expression, we will get,
\[\Rightarrow H{{E}^{2}}={{\left( \dfrac{a}{2\sqrt{2}} \right)}^{2}}+{{\left( \dfrac{a}{2\sqrt{2}} \right)}^{2}}\]
Adding up the terms in the above expression, we will get,
\[\Rightarrow H{{E}^{2}}=\dfrac{{{a}^{2}}}{8}+\dfrac{{{a}^{2}}}{8}\]
\[\Rightarrow H{{E}^{2}}=\dfrac{2{{a}^{2}}}{8}\]
\[\Rightarrow H{{E}^{2}}=\dfrac{{{a}^{2}}}{4}\]
The value of the side HE will be,
\[\Rightarrow HE=\sqrt{\dfrac{{{a}^{2}}}{4}}\]
\[\Rightarrow HE=\dfrac{a}{2}cm\]
The figure will look like this,

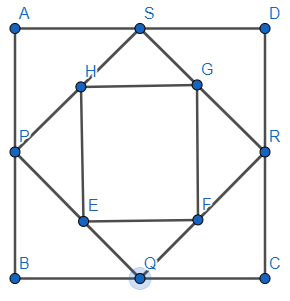
We are given that the area of the square EFGH is \[25c{{m}^{2}}\].
We have the value of the side of the square EFGH. So, we will now equate both the expressions and we get,
\[Area~of\text{ }the\text{ }square\text{ }EFGH=25c{{m}^{2}}\]
\[\Rightarrow \dfrac{a}{2}\times \dfrac{a}{2}=25c{{m}^{2}}\]
\[\Rightarrow \dfrac{{{a}^{2}}}{4}=25\]
\[\Rightarrow {{a}^{2}}=100\]
\[\Rightarrow a=10cm\]
So, we get the value of \[a=10cm\].
Now, we can substitute the value of ‘a’ in the length of the sides of the squares given to us.
The perimeter of the square ABCD = \[4(side)\]\[=4a=40cm\]
perimeter of the square PQRS = \[4(side)\] \[=4\dfrac{a}{\sqrt{2}}=2\sqrt{2}\left( 10 \right)=20\sqrt{2}cm\]
perimeter of the square PQRS = \[4(side)\] \[=4\dfrac{a}{2}=2a=20cm\]
The sum of the perimeters of the squares given to us is:
\[ABCD+PQRS+EFGH\]
\[\Rightarrow 40cm+20\sqrt{2}cm+20cm\]
\[\Rightarrow \left( 60+20\sqrt{2} \right)cm\]
Therefore, the sum of the perimeters of the given squares is \[\left( 60+20\sqrt{2} \right)cm\].

Note: The Pythagoras formula is used in the above solution as the side of a square is right angled, that is, the angle formed in the vertices is \[{{90}^{\circ }}\]. Also, the formula of the area of the square is \[{{(side)}^{2}}\] and it should be correctly written. The question asked us to find the sum of the perimeters of the squares mentioned, do not overlook the ‘sum;’ part and find only the perimeters of the squares given to us, because then it will be only partially correct.