Question

ABCD is a square plot. The angle of elevation of the top of a pole standing at D from A or C is \[{{30}^{\circ }}\] and that from B is \[\theta \] then \[\theta \] is equal to
(a) \[\sqrt{6}\]
(b) \[\dfrac{1}{\sqrt{6}}\]
(c) \[\dfrac{1}{\sqrt{3}}\]
(d) \[\dfrac{2}{\sqrt{6}}\]

Answer 1

Hint: To solve this question we will make a square and as the square has all sides equal. So we will assume its sides as the same variable ‘a’. Then we will assume a point P as the top of the pole. Joining P to square ABCD, will help to locate angle \[{{30}^{\circ }}\] & \[\theta \].
Finally using, \[\tan \theta \] = $(\dfrac{\text{perpendicular}}{\text{Base}})$ and the Pythagoras theorem gives the result. It is stated as “In a right-angled triangle the square of the hypotenuse side is equal to the sum of squares of other two sides.”

Complete step-by-step solution:
Given that ABCD is a square plot. Let us construct the square plot first.

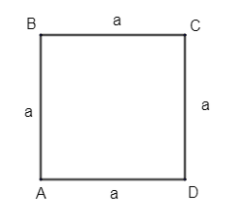
Let all sides of the square plot be of measures a.
To view the above portion of square plot ABCD we need to make a different view. Let it be as
 

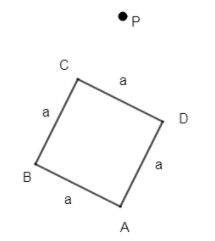
Consider P be the top of the pole, and person standing at D.
Given that angle from C is \[{{30}^{\circ }}\].
Join PC to get \[\angle PCD={{30}^{\circ }}\]. Also, \[\angle PDC={{90}^{\circ }}\] because we have a square plot and P is at top.

Let the length of side PD = h, then using the trigonometric function we have,
In \[\Delta PCD,\angle PDC={{90}^{\circ }}\] and \[\angle PCD={{30}^{\circ }}\].
As \[\Delta PCD\] is a right angled triangle at D then using \[\tan \theta \] which is equal to = $(\dfrac{\text{perpendicular}}{\text{Base}})$.
We have PD = h = perpendicular and CD = Base = a.
\[\therefore \tan \theta =\dfrac{h}{a}\]
Given that \[\theta ={{30}^{\circ }}\Rightarrow \tan {{30}^{\circ }}=\dfrac{h}{a}\].
Now we know that, \[\tan {{30}^{\circ }}=\dfrac{1}{\sqrt{3}}\].
\[\Rightarrow \dfrac{1}{\sqrt{3}}=\dfrac{h}{a}\] - (1)
Similarly, consider \[\Delta BDP\] again it is a right angle triangle, right-angled at D.
This is working on similar terms as above,
Here we are given angle at B is \[\theta \].

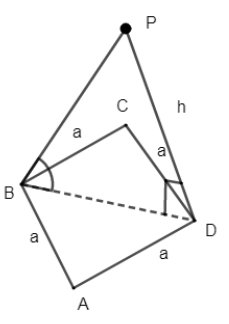
Then angle \[\angle PBD=\theta ,PD=h\] and consider, \[\Delta BCD\]; \[\angle C={{90}^{\circ }}\] and BC = a = CD.
So, it is right angled triangle,
Applying Pythagoras theorem in \[\Delta BCD\] which is stated as “In a right – angled triangle the square of the hypotenuse side is equal to the sum of squares of other two sides.”
\[\begin{align}
  & \Rightarrow {{\left( BD \right)}^{2}}={{\left( BC \right)}^{2}}+{{\left( CD \right)}^{2}} \\
 & \Rightarrow {{\left( BD \right)}^{2}}={{a}^{2}}+{{a}^{2}} \\
 & \Rightarrow {{\left( BD \right)}^{2}}=2{{a}^{2}} \\
\end{align}\]
Taking square root on both sides,
\[\Rightarrow BD=\sqrt{2}a\]
So, we have in \[\Delta BCD\],
\[\angle D={{90}^{\circ }},\angle B=\theta \] and hence applying \[\tan \theta \] on \[\theta \] angle we get,
\[\tan \theta \] = $(\dfrac{\text{perpendicular}}{\text{Base}})$
Here, Base = BD = \[\sqrt{2}a\], perpendicular, PD = h.
\[\begin{align}
  & \Rightarrow \tan \theta =\dfrac{PD}{BD}=\dfrac{h}{\sqrt{2}a} \\
 & \Rightarrow \tan \theta =\dfrac{1}{\sqrt{2}}\left( \dfrac{h}{a} \right) \\
\end{align}\]
From equation (1), substituting, \[\dfrac{h}{a}=\dfrac{1}{\sqrt{3}}\].
\[\Rightarrow \tan \theta =\dfrac{1}{\sqrt{2}}\left( \dfrac{1}{\sqrt{3}} \right)\]
\[\Rightarrow \tan \theta =\dfrac{1}{\sqrt{6}}\], which is option (b).
Therefore \[\tan \theta =\dfrac{1}{\sqrt{6}}\] is correct option.

Note: Point of confusion can be at the point where we have assumed ‘h’ to be the length of the side PD. Do not go for calculating h in terms of PD; this makes calculation lengthy and would anyway give no result. Directly assume a variable first and then try to eliminate the variable assumed at last.