Question

\[ABCD\] is a square of side $4{\text{ cm}}$.If E is a point in the interior of the square such that $\Delta CED$ is equilateral, then find the area of $\Delta ACE$ (in \[c{m^2}\]). \[\]

Answer 1

Hint:

The area of a square \[ABCD\] is \[a \times a = {a^2}\]
Diagonal of the square is \[\sqrt {{a^2} + {a^2}} = \sqrt {2{a^2}} = \sqrt 2 a\]

Let, $\Delta ABC$ be an equilateral triangle then the sides of the triangle are equal.
Suppose the sides of the triangle is a unit, then the area of the triangle is \[\dfrac{{\sqrt 3 }}{4}{a^2}\]
The height of the triangle is \[\dfrac{{\sqrt 3 }}{2}a\]
With help of the above formula we will find the area of \[\Delta ACE\].

Complete step by step answer:
It is given that, \[ABCD\] is a square of side \[4cm\].
Also, \[E\] is a point in the interior of the square such that $\Delta CED$ is equilateral,
Let \[ABCD\] be a square of side \[4cm\]

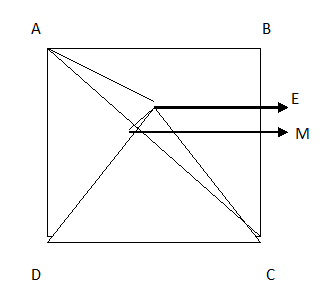
That is $AB = BC = CD = DA = 4{\text{ }}cm$
Also given that \[\Delta CED\] is an equilateral triangle.
\[EC = CD = DE = 4{\text{ }}cm\]
$\angle ECD = {60^ \circ }$  since it is the angle of an equilateral triangle
Let \[AC\] be a diagonal of the square \[ABCD\].
Therefore, \[\angle ACD{\text{ }} = {\text{ }}45^\circ \]
We know that \[\angle ECA{\text{ }} = \angle ECD{\text{ }} - \angle ACD{\text{ }}\;\]
By substituting the values of the angles we know we get,
\[\angle ECA{\text{ }} = 60^\circ {\text{ }} - {\text{ }}45^\circ = 15^\circ \]
In $\Delta ACE$, let us draw a perpendicular \[EM\] the base \[AC\].
Now in $\Delta EMC$, using the following formula we will find the value of \[EM\].
\[\sin 15^\circ = \dfrac{{EM}}{{EC}}\]
Let us substitute the value of \[EC\], we get,
\[\sin 15^\circ = \dfrac{{EM}}{4}\]
Let us substitute the value of the trigonometric function we get,
\[\dfrac{{EM}}{4} = \dfrac{{\sqrt 3 - 1}}{{2\sqrt 2 }}\]
Let us rationalize the denominator therefore we get,
\[\dfrac{{EM}}{4} = \dfrac{{(\sqrt 3 - 1) \times \sqrt 2 }}{{2\sqrt 2 \times \sqrt 2 }}\]
\[\dfrac{{EM}}{4} = \dfrac{{\sqrt 2 (\sqrt 3 - 1)}}{4}\]
Let cancel out the same terms in the above equation we get,
\[EM = \sqrt 2 (\sqrt 3 - 1)cm\]
The Diagonal of a square is \[AC\] its value is given by \[\sqrt 2 a\]
Since \[a = 4cm\] by substituting the value of a in the above equation we get,
\[\sqrt 2 a = \sqrt 2 \times 4 = 4\sqrt 2 cm\]
Hence \[AC = 4\sqrt 2 cm\]
Now let us find the area of $\Delta AEC$,
We know the area of triangle is given by the formula \[A = \dfrac{1}{2} \times {\text{height X base}}\]
In $\Delta AEC$, height is \[EM\] and base is \[AC\].
Therefore we get,
\[A = \dfrac{1}{2} \times EM \times AC\]
Let us substitute the values we know we get,
\[A = \dfrac{1}{2} \times \sqrt 2 (\sqrt 3 - 1) \times 4\sqrt 2 \]
On solving the values in the above equation we get,
\[A = \dfrac{1}{2} \times 8(\sqrt 3 - 1) = 4(\sqrt 3 - 1)c{m^2}\]
We have found the Area of \[\Delta AEC\] is \[4(\sqrt 3 - 1)c{m^2}\]
Hence, the area of \[\Delta AEC\] is \[4(\sqrt 3 - 1)c{m^2}\].

Note:
We have used the value of the \[{\text{sin }}15^\circ \].
Let us calculate the value using the formula,
\[\sin (A - B) = \sin A\cos B - \cos A\sin B\]
Now,
\[\sin 15^\circ = \sin (45^\circ - 30^\circ )\]
\[ = \sin 45^\circ \cos 30^\circ - \cos 45^\circ \sin 30^\circ \]
\[ = \dfrac{1}{{\sqrt 2 }} \times \dfrac{{\sqrt 3 }}{2} - \dfrac{1}{{\sqrt 2 }} \times \dfrac{1}{2}\]
\[ = \dfrac{{\sqrt 3 - 1}}{{2\sqrt 2 }}\]